Для преобразования равномерно распределенных случайных чисел в числа, распределенные по нормальному закону, воспользуемся преобразованием:
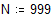
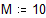

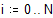
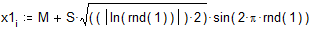
Представим числа на графике
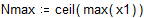
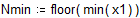

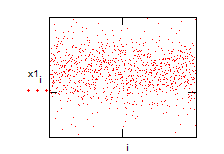
Вычислим среднее значение M1: 
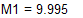
И стандартное отклонение S1: 
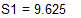
Определим функцию g(x) – функцию плотности нормального распределения с математическим ожиданием M1 и стандартным отклонением S1
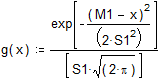
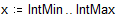
Построим гистограмму, разбив весь интервал на подынтервалы шириной 5 единиц.
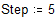

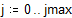
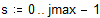
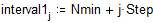



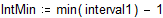
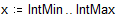
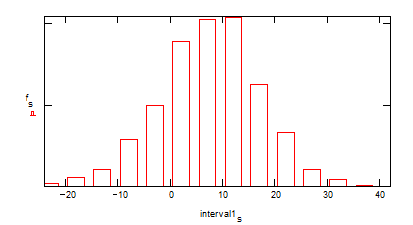
Сравним предельное распределение g(x) с реальным распределением.
Для этого вновь воспользуемся функцией hist
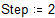

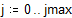
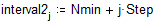

Подсчитаем плотность вероятности f1:
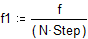


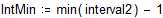
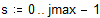
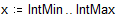
Представим результаты графически:
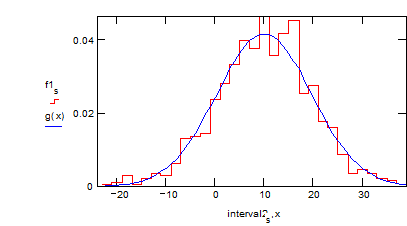
Определим вероятность W того, что некоторое число попадет в интервал [1,3], воспользовавшись функцией cnorm.
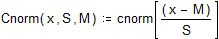
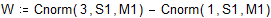
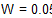
И сравним полученный результат с результатом, который дает функция hist
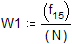
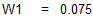
 2015-02-15
2015-02-15 953
953








