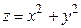Лекция 3 Функция нескольких переменных

План:

1 Функция нескольких переменных. Предел и непрерывность функция двух переменных

2 Производные и дифференциалы функции нескольких переменных

3 Производная по направлению. Градиент и его свойства

4 Экстремум функции двух переменных

5 Абсолютный и условный экстремумы. Классические методы оптимизации

3.1 Функция нескольких переменных. Предел и непрерывность функция двух переменных

При исследовании различных вопросов естественных наук приходится иметь дело с функциями двух, трех и более переменных. Введем понятие арифметического n-мерного пространства. Упорядоченную совокупность n действительных чисел 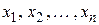называют точкой, а сами эти числа – ее координатами. Запись 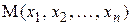означает, что точка M имеет координаты 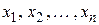. Множество всевозможных указанных точек называется арифметическим (координатным) n-мерным пространством. 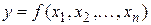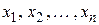Функция, определенная на некотором множестве Х арифметического n-мерного пространства называется функцией n аргументов: , где – координаты точки М данного множества. 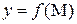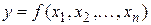В этом случае говорят, что задана функция точки М и пишут: , или , где 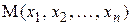– точка указанного множества. Рассмотрим случаи, когда n = 2 и n = 3. Рассмотрим фиксированную прямоугольную систему координат Oх₁х₂, в которой каждой точке M соответствует пара действительных чисел 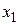и 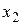. 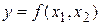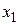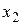Тогда функция заданная на множестве Х (некоторое множество точек плоскости), является функцией двух аргументов, то есть , где , - координаты точки .

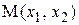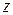Если координаты точки М обозначить буквой и , а функцию – буквой , то функция двух переменных записывается в виде . Переменные и , называются независимыми переменными, а 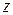- зависимой переменной (функцией).

Значение функция , которое она принимает при 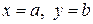, обозначается через .

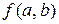Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило аналитическим способом, т.е. когда функция задана формулой.

Функцию

(1)

можно представить так: 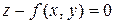, или в более общем виде

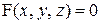(2)

Функция, заданная формулой (1), называется явной. Функция, определяемая уравнением (2), называется неявной.

Как и в случае одной независимой переменой, функция двух переменных существует, вообще говоря, не при любых значениях и .

Совокупность пар 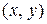значений и , при которых определяется функция , называется областью определения или областью существования этой функции.

Например, областью определения функции 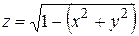является множество значений , для которых подкоренное выражение остается положительным или равным нулю: 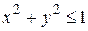, т.е. на плоскости Оху это круг с центром в начале координат и радиусом равным 1, включая окружность 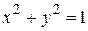, являющуюся границей области определения D. Если к области определения относятся и точки границы, то область называется замкнутой, как в данном примере. Точки области определения, не лежащие на границе, называются внутренними точками области. Область, состоящая из одних внутренних точек, называется незамкнутой или открытой. Например, для функции 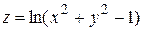областью определения является множество значений и , для которых аргумент логарифмической функции будет строго положительным 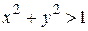. На плоскости Оху это область вне круга радиуса 1 с центром в начале координат, не включая окружность .

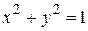Областью определения может служить и вся плоскость Оху, как например, для функции 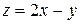, т.к. это выражение имеет смысл при любых значениях и .

Для функции трёх переменных областью определения является некоторая совокупность троек чисел 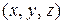. Заметим, что каждая тройка чисел задаёт некоторую точку 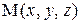в пространстве Oxyz. Таким образом, областью определения функции трёх переменных является некоторая совокупность точек пространства. Например, областью определения функции 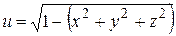является множество точек пространства Оxyz, координаты которых 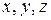удовлетворяют неравенству 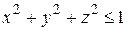, т.е. область определения это шар радиуса 1 с центром в начале координат, включая шаровую поверхность (замкнутая область).

Однако области определения функции четырёх и более переменных уже не допускают простого геометрического истолкования и не имеют простого геометрического смысла.

Перейдем к геометрическому изображению функции двух переменных. Если графиком функции одной переменной 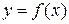в прямоугольной системе координат на плоскости Оxy является линия, то графиком функции двух переменных в прямоугольной системе координат в пространстве Оxyz является поверхность. Действительно, пусть функция определена в области D, лежащей в плоскости Оxy (рисунок 1).

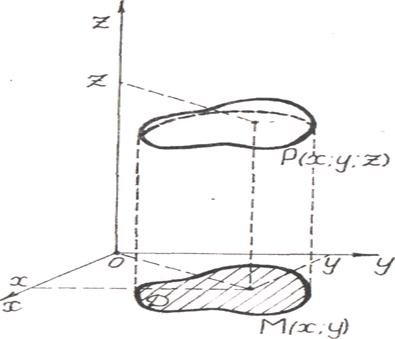
Рисунок 1. График функции

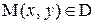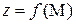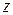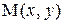Каждой точке соответствует одно определенное значение функции . Примем это значение за аппликату некоторой точки Р в системе координат Oxyz, абсцисса и ордината которой равны и . Тогда каждой точке в плоскости Оxy будет соответствовать одна определенная точка 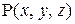в пространстве Оxyz, а всей области D-некоторое множество G точек 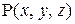, образующих некоторую поверхность. Эта поверхность называется графиком функции , т.к. 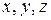координаты всех точек 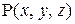этого множества G удовлетворяют уравнению .

Для исследованияхарактера поверхности используются линии уровня.

Линией уровня функции называется линия 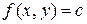на плоскости Оxy, в точках которой функция 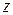сохраняет постоянное значение 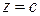. Например, для функции 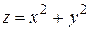линия уровня задается уравнением 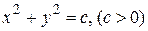т.е. является окружностью с центром в начале координат и радиусом равным 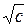. Совокупность линий уровня, соответствующих различным значениям постоянной 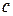, называется сетью линий уровня функции (рисунок 2).

Рисунок 2. Сеть линий уровня функции

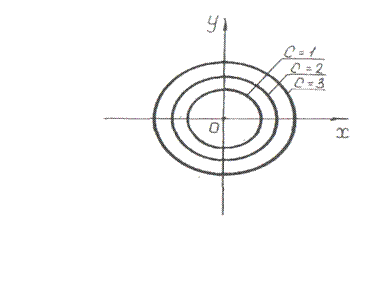
Примерами линий уровня могут служить линии равных температур (изотермы), линии равных давлений (изобары), линии равных высот суши над уровнем моря или линии равных глубин океана.

Аналогично тому, как были определены линии уровня для функции двух переменных, определим поверхности уровня для функции трех переменных. Поверхностью уровня функции 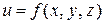называется поверхность 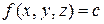в пространстве Oxyz, в точках которой функция и сохраняет постоянное значение 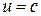. Например, для функции 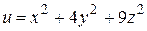поверхность уровня задается уравнением 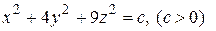или 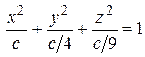т.е. является эллипсоидом с центром в начале координат и полуосями равными соответственно 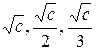(рисунок 3).

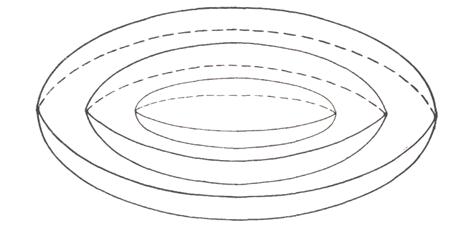
Рисунок 3 Линии уровня функци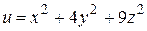и при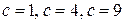

Понятие предела функции нескольких переменных вводится аналогично понятию предела функции одной переменной. Рассмотрим функцию двух переменных, так как рассмотрение трех и более переменных не вносит принципиальных изменений, но делает более громоздкими записи и формулировки. Пусть независимые переменные и неограниченно приближаются к числам 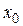и 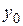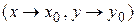, т.е точка 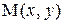неограниченно приближается к точке 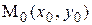на плоскости Оху 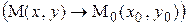. Может оказаться при этом, что существующие значения функции неограниченно приближаются к некоторому числу А, т.е. точка 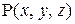в пространстве Оxyz неограниченно приближается к точке 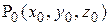с аппликатой 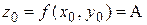(рисунок 4).

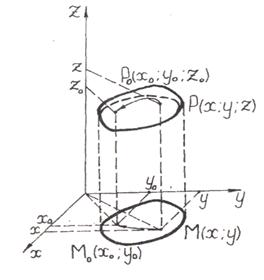
Рисунок 4

Тогда говорят, что число А есть предел функции при 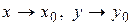. Записывается это так:

.

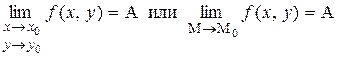При этом требуется только, чтобы функция была определена в некоторой окрестности точки 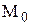, но не обязательно в самой точке 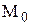. Под окрестностью точки 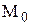понимается совокупность всех точек 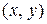, лежащих внутри круга с центром в точке 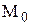и радиусом δ (δ - окрестность).

Определение 1. Число А называется пределом функци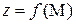и () при 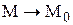, если для любого наперед заданного положительного сколь угодно малого числа ε>0, найдется такая δ - окрестность точки 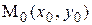, что для всех точек 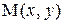этой окрестности (за исключением, быть может, точки 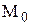) имеет место неравенство: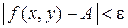

Все правила предельного перехода, установленные для функции одной переменной, остаются справедливыми для функций нескольких переменных.

Если число А является пределом функции при 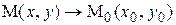то пишут: .

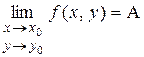Пример 1. Вычислить предел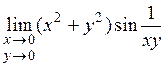

Решение: В данном случае 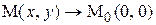, поэтому 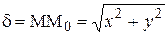и 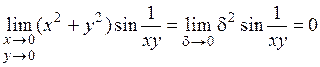т.к. произведение бесконечно малой величины 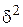на ограниченную есть бесконечно малая величина.

Пример 2. Существует ли предел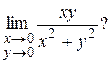

Решение. Пусть точка 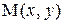стремится к точке 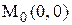по прямой 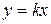, проходящей через точку 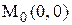. Тогда получим

.

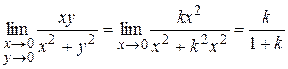Таким образом, приближаясь к точке 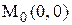по различным прямым, соответствующим разным значениям 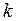, получаем разные предельные значения, зависящие от 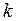. Отсюда следует, что предел данной функции в точке 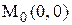не существует.

Непрерывность функции нескольких переменных определяется аналогично тому, как это делается для функции одной переменной.

Определение 2. Функция (или 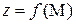) называется непрерывной в точке 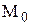, если выполнены следующие три условия:

1) функция 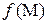определена в точке 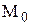и в некоторой ее окрестности;

2) существует конечный предел функции ;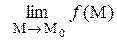

3) предел функции равен значению функции в этой точке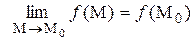

Если обозначим 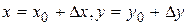, то последнее равенство можно переписать так: 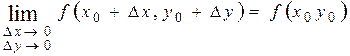или что тоже самое: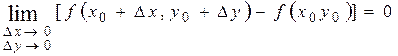

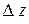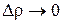Отметим, что выражение, стоящее в квадратных скобках есть полное приращение функции при , где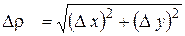

Таким образом условие непрерывности функции можно представить в виде: .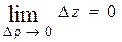

Если в точке 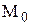хотя бы одно из этих условий (1-3) нарушено, то точка 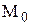называется точкой разрыва функции 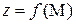. Например, функция

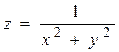является непрерывной всюду, кроме точки O(0,0), в которой функция не определена, так что точка О(0,0) является точкой разрыва функции.

С другой стороны функция 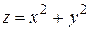непрерывна в любой точке плоскости.

Действительно: 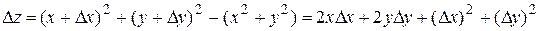и следовательно: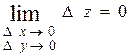

Для функции 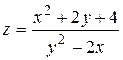точками разрыва являются точки, которые расположены на лини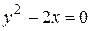и или 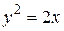, т.е. на параболе. При приближении точки 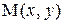к какой-либо точке этой параболы данная функция бесконечно возрастает.