Производная по направлению. Градиент и его свойства

Пусть задана функция двух переменных – непрерывная вместе с частным производными в области D, и вектор 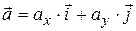. Зафиксируем точку 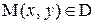и рассмотрим по направлению вектора 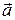точку 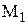, отстоящую от точки М на расстояние 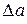(рисунок 5)

Разность 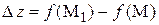определяет изменение (приращение) функции при переходе от точки М к точке М₁, а отношение 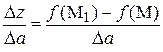определяет среднюю скорость изменения функции 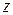на участке 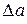. Эта средняя скорость тем точнее определяет мгновенную скорость, чем меньше .

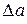Производной функции в точке 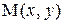М по направлению вектора 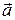называется предел отношения приращения функции 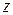в направлении 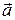к вызвавшему его приращению расстояния :

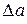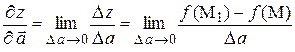
Производная по направлению 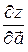является скоростью изменения функции 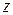по направлению вектора 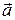в точке М. Если 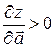, то функция возрастает в направлении 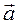со скоростью равной 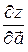, если 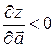, то функция 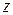убывает в направлении 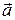со скоростью равной .

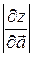Поскольку полное приращение функции равно:

,

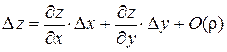где 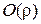- бесконечно малая более высокого порядка, чем

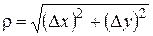, то .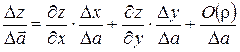

Из прямоугольных треугольников ММ₁А и ММ₁В (рисунок 5) находим:

;

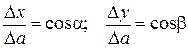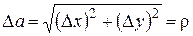
Следовательно при 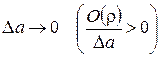получим:

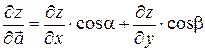, (5)

где .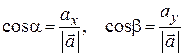

В частности, если вектор 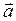сонаправлен с одной из координатных осей, то производная по направлению 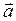совпадает с соответствующей частной производной. Например, если 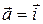, т.е. 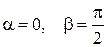, то:

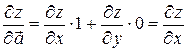
Градиентом функции в точке 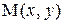называется вектор 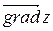, проекциями которого на оси координат являются значения частных производных 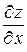и :

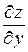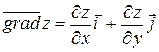(6)

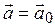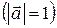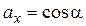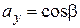Если вектор - единичный , т.е. и и 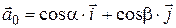, то скалярное произведение векторов 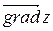и 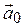равно:

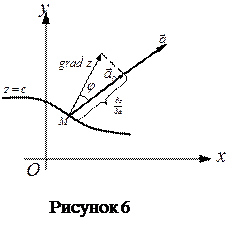
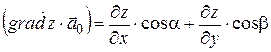
Следовательно, 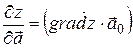, откуда 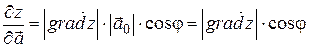, т.к.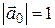

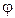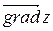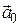Здесь - угол между векторами и в точке М (рисунок 6)

Таким образом, производная функции 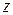по направлению вектора 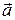равна проекции вектора 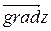на вектор :

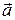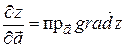
Отсюда следует, что 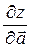принимает наибольшее значение при 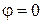, т.е. в направлении 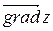в данной точке:

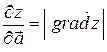
Иначе говоря, вектор 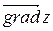в данной точке указывает направление наибыстрейшего возрастания функции 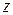в этой точке, а 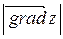определяет наибольшую скорость возрастания функции 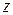в этом направлении. Наоборот, при 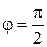, т.е. в направлении вектора 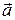, перпендикуляного к вектору 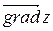, производная 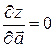, т.к. 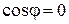и 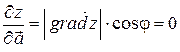, т.е. функция не изменяется в этом направлении.

Таким образом, вектор 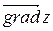направлен перпендикулярно к линии уровня 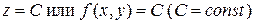, лежащей в плоскости Oху и проходящей через соответствующую точку.