Рассмотрим функцию двух переменных  . Зафиксируем значение одного из ее аргументов, например,
. Зафиксируем значение одного из ее аргументов, например,  , т.е.
, т.е. 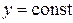 , тогда функция
, тогда функция  будет функцией одной переменной
будет функцией одной переменной  . Придадим этой переменной в точке
. Придадим этой переменной в точке 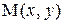 приращение
приращение 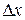 , тогда функция
, тогда функция  примет приращение
примет приращение
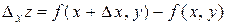 ,
,
которое называется частным приращением функции 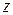 по
по  в точке
в точке 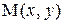 . Зафиксируем теперь аргумент
. Зафиксируем теперь аргумент  , т.е.
, т.е. 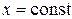 , тогда функция
, тогда функция  будет функцией одной переменной
будет функцией одной переменной  . Придадим этой переменной в точке
. Придадим этой переменной в точке 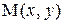 приращение ∆у, тогда функция
приращение ∆у, тогда функция  примет приращение
примет приращение
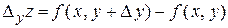 ,
,
которое называется частным приращением функции по  в точке
в точке 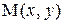 .
.
Определение 1. Частной производной по  от функции
от функции  называется предел отношения частного приращения
называется предел отношения частного приращения 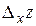 по
по  к приращению
к приращению 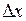 при стремлении
при стремлении 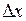 к нулю:
к нулю: 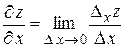 .
.
Частной производной по  от функции
от функции  называется предел отношения частного приращения
называется предел отношения частного приращения 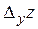 по
по  к приращению
к приращению 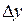 при стремлении
при стремлении 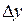 к нулю:
к нулю: 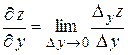 .
.
Из определения ясно, что правила вычисления частных производных совпадают с правилами вычисления производной функции одной переменной.
Пример 1. Найти частные производные
а) 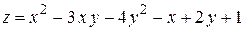 ,
,
б) 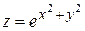 .
.
Решение. а) Рассматривая  как постоянную величину, и учитывая, что производная от постоянной равна нулю, получим:
как постоянную величину, и учитывая, что производная от постоянной равна нулю, получим: 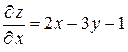
Рассматривая  как постоянную, найдем:
как постоянную, найдем: 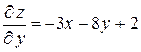
б) 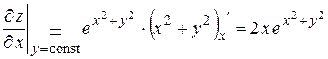 ,
,
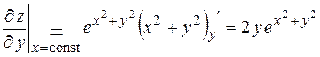 .
.
Геометрический смысл частных производных: частная производная 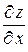 или
или 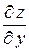 есть тангенс угла наклона касательной в точке М к кривой, получающейся в сечении поверхности
есть тангенс угла наклона касательной в точке М к кривой, получающейся в сечении поверхности  плоскостью
плоскостью 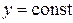 (или
(или 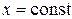 ).
).
Физический смысл частных производных: частная производная 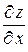 или
или 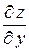
это скорость изменения функции  в точке М в направлении оси Ох (или Оу).
в точке М в направлении оси Ох (или Оу).
Пусть функция  непрерывная и имеет непрерывные частные производные первого порядка
непрерывная и имеет непрерывные частные производные первого порядка 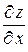 ,
, 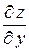 , которые являются также функциями двух переменных
, которые являются также функциями двух переменных  и
и  . Частные производные от производных первого порядка называются частными производными второго порядка от функции
. Частные производные от производных первого порядка называются частными производными второго порядка от функции  . Их четыре:
. Их четыре:
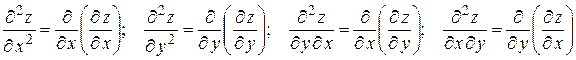 .
.
Последние две частные производные второго порядка называются смешанными. Одна из них получается дифференцированием функции сначала по  , затем по
, затем по  , а другая наоборот, - сначала по
, а другая наоборот, - сначала по  , затем по
, затем по  .
.
Теорема. Если смешанные частные производные второго порядка функции  непрерывны, то они равны между собой
непрерывны, то они равны между собой 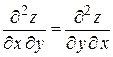 .
.
Пример 2. Найти частные производные второго порядка функций:
а) 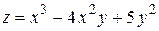 ; б)
; б) 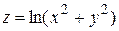
Решение: а) Найдем сначала частные производные первого порядка:
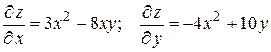 .
.
Дифференцируя производную 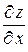 сначала по
сначала по  , затем по
, затем по  , получим:
, получим:
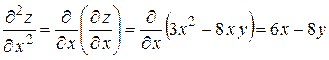 ;
;
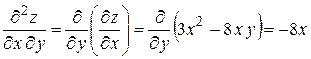 .
.
Дифференцируя производную 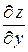 сначала по
сначала по  , затем по
, затем по  , получим:
, получим:
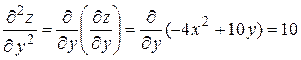 ;
;
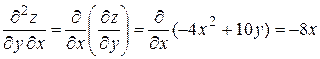 .
.
Заметим, что: 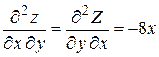 .
.
б) Найдем производные первого порядка: 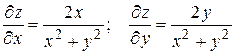 .
.
Дифференцируя производную 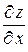 сначала по
сначала по  , затем по
, затем по  , получим:
, получим:
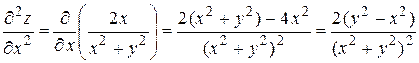
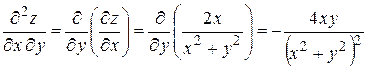
Дифференцируя производную 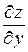 сначала по
сначала по  , затем по
, затем по  , получим:
, получим:
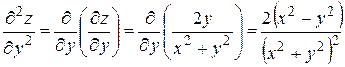 ;
;
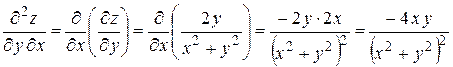 .
.
Заметим также, что и в этом случае: 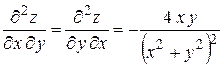 т.е. результат дифференцирования не зависит от порядка дифференцирования.
т.е. результат дифференцирования не зависит от порядка дифференцирования.
Вторые частные производные обозначаются также символами: 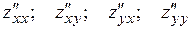 .
.
Рассмотрим функцию двух переменных  . Придадим аргументам
. Придадим аргументам  и
и  приращения
приращения 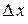 и
и  . Тогда функция
. Тогда функция  получит полное приращение
получит полное приращение 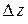 , равное:
, равное: 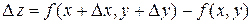 .
.
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 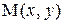 , если в некоторой окрестности этой точки полное приращение функции может быть представлено в виде
, если в некоторой окрестности этой точки полное приращение функции может быть представлено в виде 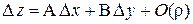 , где А, В - величины, не зависящие от
, где А, В - величины, не зависящие от 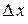 и
и  , а
, а 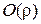 бесконечно малая величина более высокого порядка малости, чем
бесконечно малая величина более высокого порядка малости, чем 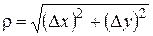 при
при 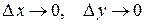 . Дифференциалом
. Дифференциалом 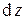 функции
функции  в точке
в точке 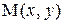 называется главная часть полного приращения
называется главная часть полного приращения 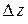 этой функции в рассматриваемой точке, линейная относительно
этой функции в рассматриваемой точке, линейная относительно 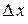 и
и  , т.е.
, т.е. 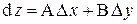
Дифференциалы независимых переменных 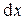 и
и 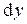 равны их приращениям:
равны их приращениям: 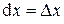 и
и 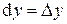 . Можно доказать, что
. Можно доказать, что 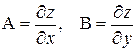 . Следовательно, дифференциал функции
. Следовательно, дифференциал функции  вычисляется по формуле:
вычисляется по формуле:
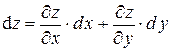 (3)
(3)
Таким образом, если функция  имеет непрерывные частные производные в точке
имеет непрерывные частные производные в точке 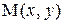 , то она дифференцируема в этой точке и ее дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных.
, то она дифференцируема в этой точке и ее дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных.
При малых приращениях аргументов 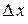 и
и  полное приращение функции
полное приращение функции 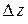 с точностью до бесконечно малой более высокого порядка, чем
с точностью до бесконечно малой более высокого порядка, чем 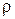 можно заменить ее дифференциалом
можно заменить ее дифференциалом 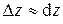 , т.е.
, т.е. 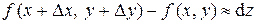 . Отсюда
. Отсюда 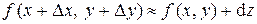 или с учётом равенства (3):
или с учётом равенства (3):
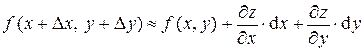 .
.
Полагая 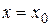 ,
, 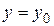 ,
, 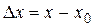 ,
, 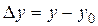 , получим
, получим
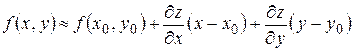 (4)
(4)
Формула (4) позволяет приближенно вычислить значения функции  в точке
в точке 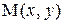 , близкой к точке
, близкой к точке 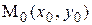 , если известны значение функции и ее частных производных в точке
, если известны значение функции и ее частных производных в точке 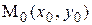 .
.
ПримерЗ. Вычислить приближенное 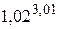 .
.
Решение: Рассмотрим функцию 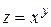 и вычислим её значение в точке
и вычислим её значение в точке 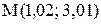 , близкой к точке
, близкой к точке 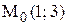 . Для этого найдём значения функции и её частных производных в точке
. Для этого найдём значения функции и её частных производных в точке 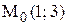 и воспользуемся формулой (4).
и воспользуемся формулой (4).
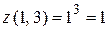 ;
; 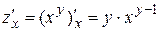 ;
; 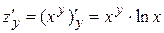 ;
; 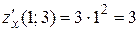 ;
; 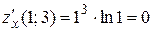 . Следовательно,
. Следовательно, 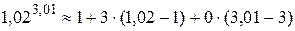 , т.е
, т.е 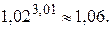
Формула (4) позволяет также линеаризовать функцию  в окрестности заданной точки
в окрестности заданной точки 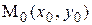 .
.
 2015-02-15
2015-02-15 4291
4291
