Преподаватель выдает каждому студенту индивидуальное задание. Исходные данные приведены на рис. 21 и табл. 21,22.
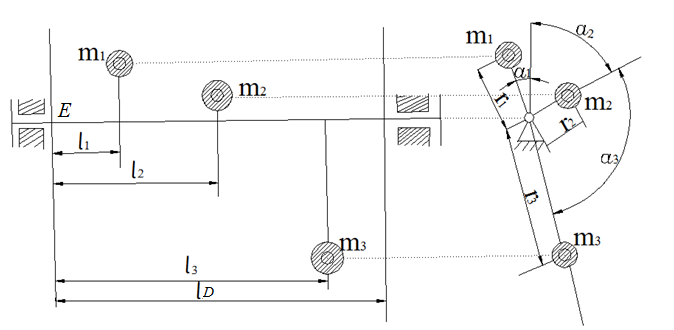
Рис 21 Схема вала с вращающимися массами
Таблица 21
| Параметры | Варианты | |||||||||
| m 1, кг | ||||||||||
| m 2, кг | ||||||||||
| m 3, кг | ||||||||||
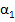 , град , град
| ||||||||||
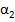 , град , град
| ||||||||||
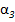 , град , град
| ||||||||||
| r 1, м | 0,1 | 0,2 | 0,1 | 0,3 | 0,4 | 0,2 | 0,1 | 0,4 | 0,15 | 0,3 |
| r 2, м | 0,1 | 0,3 | 0,2 | 0,2 | 0,3 | 0,5 | 0.3 | 0,3 | 0,2 | 0,5 |
| r 3, м | 0,4 | 0,2 | 0,3 | 0,3 | 0,15 | 0,25 | 0,2 | 0,4 | 0,35 | 0,35 |
| l 1, м | 0,2 | 0,5 | 0,8 | 0,5 | 0,3 | 0.4 | 0,3 | 0,45 | 0,4 | 0,6 |
| l 2, м | 0,5 | 0,8 | 0,9 | 0,9 | 0,8 | 0,8 | 0,7 | 0,9 | 0,85 | 0.9 |
| l 3, м | 0,8 | 1,2 | 1,1 | 1,2 | 1,3 | 0,95 | 0,9 | 1,2 | 1,1 | 1,3 |
| lD, м | 1,5 | 1,4 | 1,3 | 1,3 | 1,5 | 1,1 | 1,1 | 1,3 | 1,3 | 1,4 |
Таблица 22
| Параметры | Варианты | |||||||||
| m 1, кг | ||||||||||
| m 2, кг | ||||||||||
| m 3, кг | ||||||||||
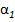 , град , град
| ||||||||||
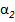 , град , град
| ||||||||||
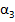 , град , град
| ||||||||||
| r 1, м | 0,15 | 0,25 | 0,2 | 0,25 | 0,45 | 0,18 | 0,2 | 0,3 | 0,3 | 0,1 |
| r 2, м | 0,2 | 0,3 | 0,1 | 0,3 | 0,4 | 0,5 | 0.4 | 0,2 | 0,3 | 0,4 |
| r 3, м | 0,2 | 0,4 | 0,2 | 0,15 | 0,25 | 0,2 | 0,3 | 0,4 | 0,35 | |
| l 1, м | 0,2 | 0,5 | 0,8 | 0,5 | 0,3 | 0.4 | 0,3 | 0,45 | 0,4 | 0,6 |
| l 2, м | 0,6 | 0,9 | 1,0 | 0,85 | 0,8 | 0,8 | 0,7 | 0,9 | 0,85 | 0.9 |
| l 3, м | 0,8 | 1,2 | 1,2 | 1,3 | 1,4 | 1,1 | 0,9 | 1,2 | 1,1 | 1,3 |
| lD, м | 1,5 | 1,4 | 1,4 | 1,5 | 1,6 | 1,3 | 1,1 | 1,4 | 1,3 | 1,6 |
Требуется:
1.Изобразить вал с заданными вращающимися массами в масштабе.
2. Выбрать один из способов полного уравновешивания нескольких масс. Определить дисбалансы всех заданных масс.
3. Выбрать плоскости расположения противовесов: первую – левее всех заданных масс, т.е. ближе к левой опоре; вторую – правее, т.е. ближе к правой опоре вала.
4. Подсчитать моменты всех дисбалансов относительно точки Е, лежащей в левой крайней плоскости.
5. Сложить геометрически все моменты, т.е. построить многоугольник моментов. Замыкающий вектор этого многоугольника – момент дисбаланса противовеса, уравновешивающего всю систему динамически.
6. Зная величину плеча (расстояние между плоскостями противовесов 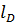 ), определить дисбаланс, задать радиус
), определить дисбаланс, задать радиус 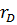 и найти массу противовеса, установленного в крайней правой плоскости.
и найти массу противовеса, установленного в крайней правой плоскости.
7. Показать положение противовеса 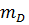 на обеих проекциях. Система стала уравновешена динамически.
на обеих проекциях. Система стала уравновешена динамически.
8. Для уравновешивания системы статически построить многоугольник дисбалансов и замкнуть его. Замыкающий вектор представляет собой дисбаланс противовеса, уравновешивающего систему статически.
9. Задать радиус массы 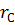 и определить массу противовеса, которую помещают в левой крайней плоскости
и определить массу противовеса, которую помещают в левой крайней плоскости 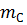 .
.
10. Результаты расчетов свести в таблицу, которая прилагается к отчету:
| Массы | r, м | 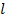 , м , м
| 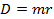 , кг м , кг м
| 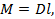 кг кг  м2 м2
| 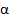 , град , град
|
m 1, кг
m 2, кг
m 3, кг
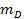
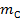
|
 2015-02-15
2015-02-15 610
610








