Законы коммутации

Переходный процесс − это процесс, возникающий в электрической цепи, при переходе от одного установившегося режима к другому. Этот переход может быть вызван различными причинами:

− изменением структуры цепи (исключением отдельных элементов цепи или включением в цепь новых элементов);

− изменением параметров источников (например, изменением величины постоянной ЭДС, изменением амплитуды, частоты или фазы переменной ЭДС);

− изменением параметров элементов цепи (например, изменением числа витков катушки индуктивности).

Переходный процесс имеет место, например, при подключении какой-либо электрической цепи к источнику питания, или в случае возникновения аварийных ситуаций − выхода из строя какого-либо элемента, короткого замыкания и т.п. Причину возникновения переходного режима принято называть коммутацией, причем время ∆ t, в течение которого она происходит, бесконечно мало, т.е. ∆ t =0. Момент времени, предшествующий коммутации, обозначают t ₋₀, а момент времени, непосредственно прилегающей к коммутации, но после ее осуществления, обозначают t ₊₀. Аналогичными индексами обозначают токи и напряжения в цепи в соответствующие моменты времени, например, i ₋₀, u ₋₀ и i ₊₀, u ₊₀.

Возникновение переходного процесса связано с наличием в электрических цепях элементов, запасающих энергию электромагнитного поля − индуктивностей и емкостей. Если электрическая цепь содержит только активные сопротивления, то переходный процесс в цепи не возникает, а переход от одного установившегося режима к другому происходит мгновенно. Это связано с тем, что в индуктивности и емкости происходит накопление энергии, а при переходе из одного установившегося режима в другой происходит перераспределение энергии электрического поля в емкости и магнитного поля в индуктивности.

В любой электрической цепи не могут развиваться бесконечно большие напряжения или протекать бесконечно большие токи. Это потребовало бы источников энергии бесконечно большой мощности, что физически невозможно. Поэтому мгновенная мощность p − всегда величина конечная.

Если изменение энергии W в емкости или индуктивности во время коммутации за время ∆ t →0 обозначим ∆ W = W ₊₀− W ₋₀, то получим:

∆ W = p ∆ t →0, (6.1)

откуда следует равенство W ₊₀= W ₋₀.

Поскольку энергия магнитного поля в индуктивности W_L и электрического поля в емкости W_C соответственно равны:

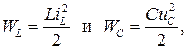
то, согласно выражению (6.1), изменения напряжения на емкости u_C и тока i_L в индуктивности в момент коммутации не происходит, т.е.

i_{L− 0}= i_{L+ 0} и u_{C −0}= u_{C +0}.

Полученные равенства выражают первый и второй законы коммутации:

Первый закон коммутации: ток через индуктивность непосредственно до коммутации равен току через ту же индуктивность после коммутации.

Второй закон коммутации: напряжение на емкости непосредственно до коммутации равно напряжению на той же емкости после коммутации.

Другими словами, ток в индуктивности и напряжение на емкости не могут меняться скачком.

Если говорить в более обобщенном смысле о процессе коммутации, то переходный режим также может возникать и при скачкообразном изменении как емкости, так и индуктивности при наличии индуктивной связи между контурами. Поэтому строго говоря в момент коммутации не может скачком измениться суммарное потокосцепление обмоток и суммарный заряд на емкостях электрической цепи.

Величины i_{L+ 0} и u_{C +0} являются начальными значениями, от которых в переходном процессе происходит изменение тока в индуктивности и напряжения на емкости. Поскольку они соответствуют значениям установившегося режима до коммутации и соответственно не зависят от характера самой коммутации, то их принято называть независимыми начальными условиями.

В течение переходного процесса токи и напряжения на элементах цепи изменяются. Для расчета переходного процесса составляют уравнения по законам Кирхгофа для мгновенных значений токов и напряжений и решают их. Учитывая, что связь между токами и напряжениями на реактивных элементах выражается через производную 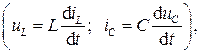расчет переходных режимов связан с решением дифференциальных уравнений. Порядок уравнения определяется числом реактивных элементов в цепи. Если в цепи имеется одна индуктивность или емкость, то получается уравнение первого порядка, а цепь называется цепью первого порядка. Если цепь содержит одну индуктивность и одну емкость, две индуктивности или две емкости, то получается уравнение второго порядка, а цепь называют цепью второго порядка, и т.д.

В связи с этим представляется целесообразным напомнить основные положения теории линейных дифференциальных уравнений.

6.1.2. Сведения из теории линейных

дифференциальных уравнений

Переходные процессы в линейных электрических цепях описываются неоднородными линейными дифференциальными уравнениями с постоянными коэффициентами. В настоящем пособии рассматриваются переходные процессы в цепях постоянного тока не выше второго порядка, поэтому остановимся лишь на основных положениях теории уравнений первого и второго порядка применительно к решаемым задачам.

Линейное неоднородное дифференциальное уравнение первого порядка с постоянными коэффициентами имеет вид

y ′+ qy = F ₁, (6.2)

где y − искомая функция, зависящая от времени; q − постоянный коэффициент; F ₁ − некоторая функция от времени.

Дифференциальное уравнение второго порядка имеет вид

y ′′+ py ′+ qy = F ₂, (6.3)

где y − искомая функция, зависящая от времени; p,q − постоянные коэффициенты; F ₂ − некоторая функция от времени.

При расчете переходных процессов за искомую функцию принимают либо ток в индуктивности i_L (t), либо напряжение на емкости u_C (t), которые называют переменными состояния. Такое название обусловлено тем, что именно процессы в реактивных элементах определяют характер переходного процесса. Так как согласно законам коммутации ток в индуктивности и напряжение на емкости до и после момента коммутации не меняют своих значений, то это позволяет просто найти начальные условия при решении дифференциальных уравнений.

Для того, чтобы была понятна связь между дифференциальными уравнениями и переходными режимами в электрических цепях, примем в качестве искомой функции ток в индуктивности i_L (t). Тогда уравнения (6.2) и (6.3) примут вид

i_L ′(t)+ qi_L (t)= F ₁; (6.4)

i ′′ _L (t)+ pi_L ′(t)+ qi_L (t)= F ₂. (6.5)

Функции F ₁ и F ₂ для линейных цепей постоянного тока представляют собой постоянные, определяемые параметрами источников энергии и структурой цепи.

Известно, что решением каждого из уравнений (6.4) и (6.5) является сумма двух составляющих:

i_L (t)= i _общ(t)+ i _ч, (6.6)

где i _общ(t) − общее решение однородного уравнения_., которое получается из уравнений (6.4) и (6.5) при F ₁=0 и F ₂=0; i _ч − частное решениеуравнений (6.4) и (6.5).

Рассмотрим порядок решения уравнений.

1. Решение дифференциального уравнения первого порядка (6.4).

Соответствующее однородное уравнение имеет вид:

i_L ′(t)+ qi_L (t)=0. (6.7)

Из теории дифференциальных уравнений известно, что общее решение i _общ(t) линейного однородного уравнения первого порядка ищется в виде показательной функции:

i _общ(t)= Ce^kt,

где C − произвольная постоянная; k − корень характеристического уравнения.

Характеристическое уравнение получается из уравнения (6.7) заменой операции дифференцирования умножением на характеристическое число k:

k i_L (t)+ qi_L (t)=0.

Сокращая на i_L (t), получим стандартный вид характеристического уравнения

k + q = 0.

Корень полученного уравнения k = − q. Тогда общее решение запишется в виде:

i _общ(t)= Ce^−qt. (6.8)

Частным решением i _ч является любое конкретное значение переменной i (t), которое при подстановке в исходное уравнение (6.4) дает тождество.

Применительно к переходным процессам в электрических цепях в качестве частного решения принимают установившееся значение рассматриваемой переменной, в данном случае − ток I_{L уст} в индуктивности. Действительно, математическим условием достижения установившегося режима является требование t→∞. Поскольку выражение (6.6) дает величину тока в любой момент времени после коммутации, в том числе и в установившемся режиме, то, подставляя (6.8) в (6.6) и полагая t→∞, получим:

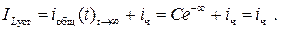
В цепях постоянного тока установившееся значение тока − величина постоянная, поэтому из уравнения (6.4) следует очевидное равенство:

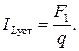
Таким образом, решением уравнения первого порядка будет выражение

i_L (t)= Ce^−qt + I_{L уст}. (6.9)

Осталось найти постоянную С. Она находится из начального условия, т.е. по значению переменной i_L (t) (тока в индуктивности) при t= t ₊₀=0. Полагая известным начальное значение тока i_L (t ₊₀)= i_{L +0}, и подставляя его в выражение (6.9), получим

i_{L +0}= Ce^{−q 0}+ I_{L уст}= C+ I_{L уст},

откуда находим C= i_{L +0} − I_{L уст}.

Уравнение решено.

2. Решение дифференциального уравнения (6.5) второго порядка.

Соответствующее однородное уравнение имеет вид

i ′′ _L (t)+ pi_L ′(t)+ qi_L (t)=0. (6.10)

Характеристическое уравнение:

k ²+ pk+q= 0.

Как известно, данное квадратное уравнение имеет два корня:

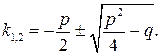
В зависимости от знака подкоренного выражения возможны три варианта:

− оба корня вещественные и разные: k ₁≠ k ₂, если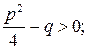

− корни вещественные и одинаковые: k ₁= k ₂, если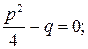

− корни комплексные сопряженные: k _1,2=α ± j ω₀, где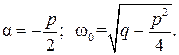

Соответствующие выражения для общих решений уравнения (6.10) приведены в табл. 6.1.

Общие решения уравнения второго порядка Таблица 6.1

Вид корней	Вид общего решения
Вещественные и разные k 1≠ k 2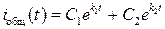
Вещественные и одинаковые k 1= k 2= k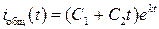
Комплексные сопряженные k 1,2=α ± j ω0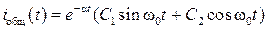

Решением уравнения (6.5) является сумма общего и частного решений:

i_L (t)= i _общ(t)+ i _ч. (6.11)

Общее решение берется из табл. 6.1 в соответствии с видом корней характеристического уравнения. Частное решение i _ч представляет собой установившееся значение тока в индуктивности: i _ч= I_{L уст}.

Для определения произвольных постоянных C ₁ и C ₂ необходимо знать начальные значения тока i_L (t ₊₀)= i_{L +0} и его производной i′_L (t ₊₀)= i′_{L +0}. Их определение рассмотрим дальше на примере решения конкретных задач, а сейчас полагаем их известными. Тогда для определения произвольных постоянных C ₁ и C ₂ следует составить два уравнения для момента времени t= t ₊₀=0. Составим их для случая вещественных и разных корней k ₁≠ k ₂.

В уравнение (6.11) подставим соответствующее выражение для общего решения и установившееся значение I_{L уст} тока и положим t= t ₊₀=0. В результате получим:

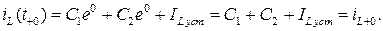
Продифференцируем уравнение (6.11) с учетом вида общего решения:

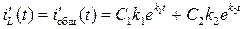
и положим t= t ₊₀=0. Тогда

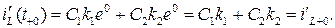
Решаем систему из полученных уравнений:

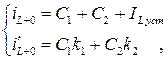
откуда найдем постоянные C ₁ и C ₂.

Окончательно решение уравнения (6.5) запишется в виде:

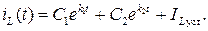
Так как установившееся значение тока − величина постоянная, то из уравнения (6.5) следует очевидное равенство:

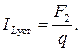
Уравнение решено.

Для двух других видов корней характеристического уравнения произвольные постоянные находятся аналогично.

Таким образом, решение неоднородного дифференциального уравнения сводится к решению характеристического уравнения и нахождению произвольных постоянных по начальным условиям с учетом параметров установившегося режима после коммутации.

6.1.3. Расчет начальных условий