Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяеться. Поэтому нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени, но можно подсчитать число молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v1 и v2. На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Согласно распределению Максвелла, вероятное число молекул в единице объема; компоненты скоростей которых лежат в интервале от 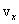 до
до 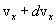 , от
, от 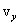 до
до 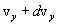 и от
и от 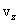 до
до 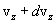 , определяются функцией распределения Максвелла
, определяются функцией распределения Максвелла
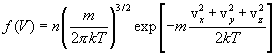
где m - масса молекулы, n - число молекул в единице объема. Отсюда следует, что n число молекул, абсолютные значения скоростей которых лежат в интервале от v до v + dv, имеет вид
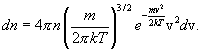
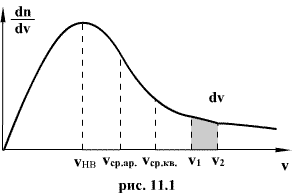
Распределение Максвелла достигает максимума при скорости 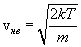 , т.е. такой скорсти, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.
, т.е. такой скорсти, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.
Кривая распределения Максвелла позволит найти среднюю арифметическую скорость
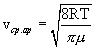 .
.
Таким образом,
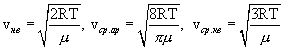 | (11.1) |
С Повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.
ДЛИНА СВОБОДНОГО ПРОБЕГА (точнее, средняя длина свободного пробега) - ср. расстояние, к-рое проходит частица между двумя последоват. столкновениями. Д. с. п.- важное понятие кинетической теории газов, введённое P. Клаузиусом (R. Clausius) в 1858.
Д. с. п. равна 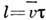 , где
, где 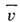 - ср. скорость молекул,
- ср. скорость молекул, 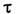 - ср. время между столкновениями, причём
- ср. время между столкновениями, причём 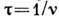 ,
, 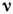 - частота столкновений, т. е. ср. число столкновений, испытываемых молекулой за единицу времени в единице объёма. Следовательно,
- частота столкновений, т. е. ср. число столкновений, испытываемых молекулой за единицу времени в единице объёма. Следовательно, 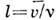 . Для газа упругих сфер радиуса а частота столкновений
. Для газа упругих сфер радиуса а частота столкновений 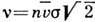 , где п - число молекул в единице объёма,
, где п - число молекул в единице объёма, 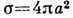 - полное эфф. сечение столкновения,
- полное эфф. сечение столкновения, 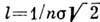 .
.
В общем случае частота столкновений равна 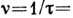
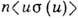 , где и - модуль относит. скорости,
, где и - модуль относит. скорости,
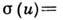
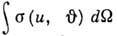 - полное эфф. сечение столкновений,
- полное эфф. сечение столкновений,
угл. скобки означают усреднение по Максвелла распределению относительных скоростей с приведённой массой 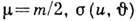 -дифференц. эфф. сечение столкновения. При вычислении кинетических коэф. оказываются существенными т. н. транспортные Д. с. п. Напр., для диффузии вводят транспортное эфф. сечение
-дифференц. эфф. сечение столкновения. При вычислении кинетических коэф. оказываются существенными т. н. транспортные Д. с. п. Напр., для диффузии вводят транспортное эфф. сечение
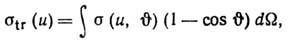
а для вязкости
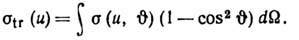
Понятие Д. с. п. удобно для качеств. рассмотрения явлений переноса в газах, оно обобщено на случай систем слабовзаимодействующих частиц: электронный газ в металлах и полупроводниках, нейтроны в слабопоглощающих средах и т. п.
Д. с. п. заряженных частиц (электронов и ионов). При классич. рассмотрении понятия полного эффективного сечения и Д. с. п. по отношению к упругим столкновениям заряж. частиц теряют смысл, поскольку за-ряж. частицы взаимодействуют между собой на сколь угодно больших расстояниях r. Квантовая механика, основываясь на соотношениях неопределённостей, даёт конечное значение для 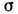 и l, если взаимодействие убывает быстрее, чем 1/ r 3. В плазме существен эффект экранирования кулоновского поля заряда на расстояниях, определяемых дебаевским радиусом зкранирования.
и l, если взаимодействие убывает быстрее, чем 1/ r 3. В плазме существен эффект экранирования кулоновского поля заряда на расстояниях, определяемых дебаевским радиусом зкранирования.
В плазме с электронной темп-рой Те и плотностью электронов N (плотность ионов при этом равна N/Zi, где Zi - ср. заряд ионов) Д. с. п. электронов по отношению к электрон-электронным столкновениям равна 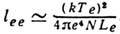 , здесь е - заряд электрона и Le - кулоновский логарифм, зависящий от Те и дебаевского радиуса. Д. с. п. электронов по отношению к электрон-ионным столкновениям в Zi раз меньше и составляет
, здесь е - заряд электрона и Le - кулоновский логарифм, зависящий от Те и дебаевского радиуса. Д. с. п. электронов по отношению к электрон-ионным столкновениям в Zi раз меньше и составляет 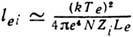 Д. с. п. ионов по отношению к ионионным столкновениям:
Д. с. п. ионов по отношению к ионионным столкновениям: 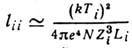 , где Ti - ионная темп-pa, Li - кулоновский логарифм с ионными величинами вместо электронных.
, где Ti - ионная темп-pa, Li - кулоновский логарифм с ионными величинами вместо электронных.
 2015-02-18
2015-02-18 3353
3353
