2015-02-18
4811
Магнитная индукция бесконечно длинного прямого повода с током находится по формуле (3.6.3). Проведем через точку наблюдения, отстоящую от проводя на произвольное расстояние R окружность L концентричную проводу (см рис.3.6.1, ток направлен на нас). На всей этой окружности значение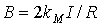 
неизменно, а сам вектор B направлен по касательной к окружности (Bl = B). Поэтому циркуляция вектора B по окружности вычисляется просто:
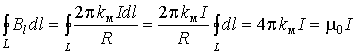. (3.7.1)
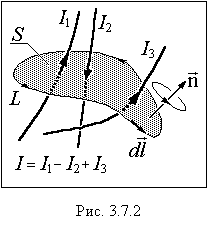
Как видим, циркуляция B не зависит от радиуса окружности, а определяется только током, охваченным ею. Можно показать, что это свойство магнитного поля остается справедливым и для случая произвольного по форме контура интегрирования L, а также в том случае, когда через площадь S (см. рис.3.7.2), охваченную контуром протекают несколько токов, т. е. выполняется, так называемый, закон полного тока:
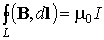. (3.7.2)
При этом под I подразумевается алгебраическая сумма этих токов. Знак плюс в этой сумме соответствует токам, направление которых связано с направлением обхода контура (т.е. выбором направления вектора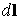 
в левой части (3.7.2)) правилом буравчика (правого винта). Токи противоположного направления входят в суммарный ток, обозначенный в формуле (3.7.2) через I, со знаком минус (см. ток I2 на рис.3.7.2). Закон полного тока в форме (3.7.2) выполняется не только для прямолинейных проводов с токами, но и для произвольных (криволинейных) токов.
Применим закон полного тока для бесконечно малой окружности площадью dS, через которую протекает бесконечно малый ток dI. Используя формулу, выражающую ток через площадку через плотность тока, т.е. dI =j dS, и выражение ротора векторного поля через циркуляцию по бесконечно малой окружности (см. формулу(1.5.3)), получим закон полного тока в дифференциальной форме:
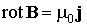. (3.7.3)
Формула (3.7.3) указывает на то, что ротор магнитного поля не равен тождественно нулю, как это имеет место для электростатического поля. Поэтому вектор магнитной индукции в области, где протекают токи, не является градиентом никакой скалярной функции (см. (1.5.6)).
Итак, в области, где протекают токи, ротор магнитного поля отличен от нуля. Это означает, во-первых, что изображение магнитного поля магнитными силовыми линиями в этой области невозможно (силовая линия не может проходить через точку, где ротор не равен нулю, а как бы полностью стягивается в эту точку). Во-вторых, не может быть введен и потенциал магнитного поля, т.к. в области, где протекают токи, не существует скалярной функции такой, что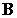 
равно ее градиенту. Это свидетельствует о непотенциальности магнитного поля.
Сравним дифференциальные уравнения для магнитного поля с дифференциальными уравнениями, описывающими электростатическое поле (в пустоте):
, 
;
, 
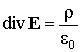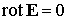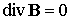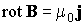. (3.7.4)
Дивергенция электростатического поля не равна нулю в области источников. Силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных. Дивергенция магнитного поля везде равна нулю. Магнитные силовые линии вне источников магнитного поля замкнуты (в области источников поля вообще не имеют смысла). Ротор электростатического поля, как и его циркуляция, тождественно равен нулю. В любой точке вектор напряженности электростатического поля выражается через градиент некоторой скалярной функции, называемой потенциалом. Электростатическое поле потенциально. Ротор В не равен нулю в области источников. Из-за этого и циркуляция В не равна нулю в этой области. Вектор В не является градиентом никакой скалярной функции координат. Магнитное поле, таким образом, непотенциально (является вихревым). В дальнейшем будет установлено, что электростатическое и магнитное поля представляют собой две стороны одной и той же объективной реальности – электромагнитного поля, которое, таким образом, в общем случае, содержит потенциальную и вихревую составляющие.
Итак, электрические токи (направленное движение заряда) создают магнитное поле, а нескомпенсированные заряды – электростатическое поле. Внутри проводника имеется электрическое поле из-за наличия ЭДС в цепи с током. Оно связано с плотностью тока уравнением (3.2.3). Вокруг проводника имеется магнитное поле, которое находится с помощью закона Био-Савара-Лапласа (3.6.2).
Покоящийся заряд не создает в окружающем пространстве магнитного поля. Заряд, движущийся с некоторой постоянной скоростью относительно выбранной системы отсчета, можно трактовать как ток. Очевидно, такой заряд создает вокруг себя и электрическое и магнитное поля. Заряд, движущийся с ускорением, создает электромагнитное поле в виде электромагнитных волн. Ниже электромагнитные волны будут рассмотрены как отдельное явление.
