








 1
1 
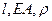
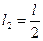
 2
2
Стержень длиной 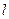 , жесткость ЕА и плотностью материала
, жесткость ЕА и плотностью материала 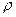 рассматривается собственным весом.
рассматривается собственным весом.
МКЭ найти напряжение стержня.
1. Выберем тип КЭ.
Так как стержень работает в условиях растяжения/сжатия, то принимаем одномерный стержневой элемент слинейной аппроксимацией продольного перемещения.
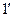
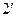




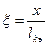
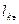
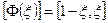 - матрица функции формы
- матрица функции формы
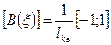
Матрица жесткости элемента:
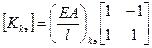
Вектор узловых перемещений:
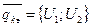
2. Сетка КЭ.
Примем, что стержень разбит на два конечных элемента.
Матрица индексов:
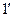 | ||
 |
Свойства конечного элемента:
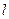 | 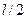 | 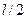 |
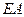 | 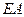 | 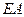 |
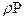 | 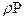 | 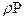 |
Закрепление узла:
| № | Код закрепления |
3. формирование матричных характеристик ансамбля.
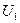 | 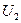 | 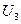 | |
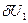 | 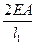 | 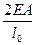 | |
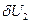 | 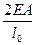 | 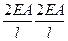 | 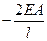 |
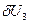 | 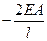 | 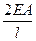 |
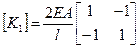
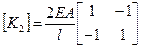
Формирование вектора нагрузки.
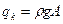 - распределенная нагрузка, собственный вес стержня
- распределенная нагрузка, собственный вес стержня
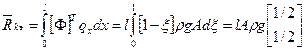
Вычисление вектора узловых сил ансамбля.
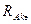
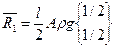
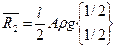
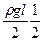 |
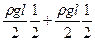 |
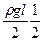 |
4. Решение системы уравнений.
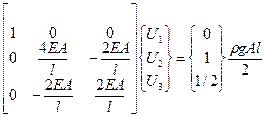
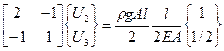
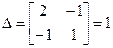
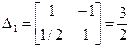
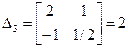
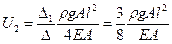
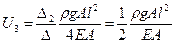
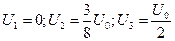
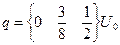
5. Вычисление напряжения в стержнях.
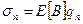
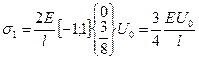
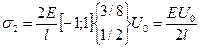
6. Построение эпюр перемещения и напряжения.






 1 ¾ ¾
1 ¾ ¾


 3/8
3/8


 ¾ ½
¾ ½





 2
2



 ¼ ¼
¼ ¼



 3
3

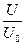
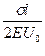
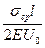
Эпюра напряжения показывает, что граничные условия в напряжениях 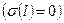 при наличии распределенной нагрузки и линейных функциях формы не выполняется.
при наличии распределенной нагрузки и линейных функциях формы не выполняется.
При увеличении количества КЭ ошибка в напряжениях на свободном конце уменьшается, но нулем никогда не будет.
Можно существенно уменьшить эту ошибку, если изменить порядок полиномов в функции формы. Для данной задачи можно практически устранить эту ошибку, если применять функции формы в виде полиномов второй степени.
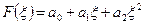
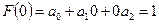
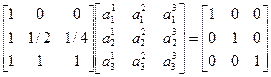
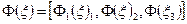
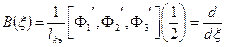
В задачах динамики деформированного твердого тела силы инерции, связанные с перемещениями точек, сопоставимы с величинами нагрузки. Поэтому основное отличие задач динамики заключается в том, что в системе уравнений МСС учитываются силы инерции, вместо уравнений равновесия используются уравнения движения.
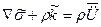
Применительно к стержням можно определить силы инерции, связанные с различными видами движений поперечного сечения с поступательными перемещениями центра тяжести сечения и его поворотами.
Удобно для постановки задачи динамики использовать вариационное уравнение Лагранжа. Его отличием от статического варианта будет добавление в число объемных нагрузок сил инерции:
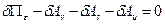
Последнее слагаемое - элементарная работа сил инерции – записывается в виде:
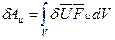

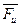 - сила инерции Доломбера
- сила инерции Доломбера
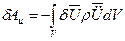 (2.82)
(2.82)
Статические гипотезы Бернули не входят в это уравнение.
Кинематические гипотезы:
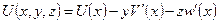
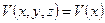
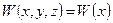
Последние три соотношения выражают компоненты перемещений при наложении пространственного изгиба на растяжение/сжатие. При кручении справедливо соотношение:
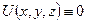
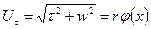 , где r – радиальная координата
, где r – радиальная координата
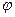 - угол закручивания поперечного сечения
- угол закручивания поперечного сечения
Как и в статике, благодаря выбору системы координат, состояние стержня определяется суперпозицией растяжения, кручения и двух плоских изгибов.
Поэтому выражение для элементарных работ сил инерции удобно рассматривать для каждого из простейших состояний.
Растяжение/сжатие: 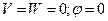
Элементарная работа сил инерции:
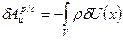
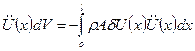
Вариационное уравнение динамики растяжения/сжатия:
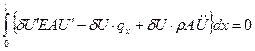 (2.83)
(2.83)
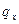 - продольная константа распределения нагрузки
- продольная константа распределения нагрузки
Из этого уравнения нетрудно получить дифференциальное уравнение движения в перемещениях.
Вычислим первый интеграл по частям.
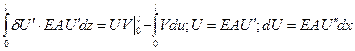
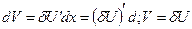 тогда
тогда
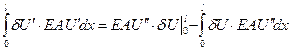
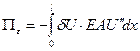
Подставляя в вариационное уравнение, получим:
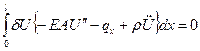
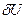 - малый, не равный нулю множитель, следовательно
- малый, не равный нулю множитель, следовательно
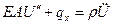 (2.84)
(2.84)
К этому уравнению следует присоединить начальные и граничные условия.
Плоский изгиб:
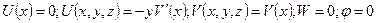
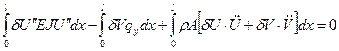 (2.85)
(2.85)
Преобразуем это уравнение, чтобы получить дифференциальное уравнение движения при плоском поперечном изгибе
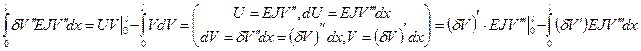 =
=
= 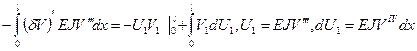
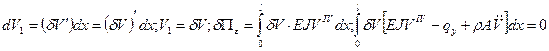
Поучаем уравнение состояния
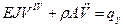 (2.86) - дифференциальное уравнение движения при плоском поперечном изгибе.
(2.86) - дифференциальное уравнение движения при плоском поперечном изгибе.
В этом уравнении мы пренебрегали силами инерции, связанными с продольными перемещениями, т.е. с поворотами сечения.
Покажем, что такое пренебрежение допустимо для тонких стержней.
Рассмотрим составляющую

Запишем полное выражение для работы сил инерции
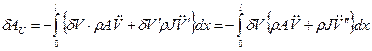
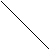
Перейдем к безразмерной координате 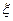 , так что
, так что 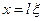 , тогда
, тогда 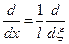
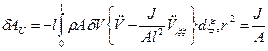 - радиус инерции поперечного сечения
- радиус инерции поперечного сечения
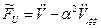 - сила инерции
- сила инерции
В последнем выражении выделяются две составляющие силы инерции: первая – инерция поперечного перемещения, а вторая – инерция поворота поперечного сечения. Инерция поворота по сравнению с инерцией поперечного перемещения дает поправку порядка 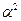 . Если определить тонкий стержень как стержень, у которого наибольший поперечный размер имеет порядок 0,1 по отношению к длине, то верхняя оценка погрешности вносимой пренебрежением инерцией поворота равна 0.01. Следовательно, для тонких стержней инерцией поворота можно пренебречь.
. Если определить тонкий стержень как стержень, у которого наибольший поперечный размер имеет порядок 0,1 по отношению к длине, то верхняя оценка погрешности вносимой пренебрежением инерцией поворота равна 0.01. Следовательно, для тонких стержней инерцией поворота можно пренебречь.
Кручение.
Вариационное уравнение Лагранжа
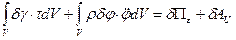
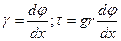
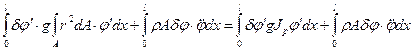
Выражение для потенциальной энергии деформации и работы сил инерции при кручении того же типа, что и при растяжении. Поэтому разрешающие дифференциальные уравнения для кручения будут такого же вида как при одноосном растяжении, 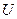 заменяем на
заменяем на 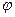 а
а 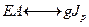
Для однозначного решения задачи следует поставить начальные и краевые условия.
 2015-02-18
2015-02-18 1068
1068








