Построение КА по регулярной грамматике

Вход: Регулярная грамматика .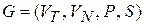

Выход: КА .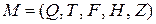

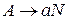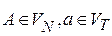Шаг 1. Пополнить грамматику правилом , где и 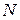- новый нетерминал, для каждого правила вида 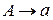, если в грамматике нет соответствующего ему правила 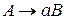, где .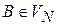

Шаг 2. Начальный символ грамматики 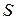принять за начальное состояние КА 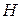. Из нетерминалов образовать множество состояний автомата 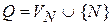, а из терминалов – множество символов входного алфавита .

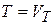Шаг 3. Каждое правило 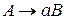преобразовать в функцию переходов 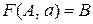, где .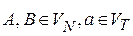

Шаг 4. Во множество заключительных состояний включить все вершины, помеченные символами 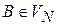из правил вида 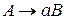, для которых имеются соответствующие правила 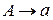, где .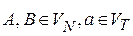

Шаг 5. Если в грамматике имеется правило 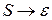, где 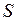- начальный символ грамматики, то поместить 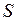во множество заключительных состояний.

Шаг 6. Если получен НКА, то преобразовать его в ДКА.

Пример Дана регулярная грамматика 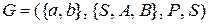с правилами 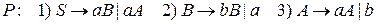. Построить по регулярной грамматике конечный автомат.

Решение задачи состоит из следующей последовательности действий.

1 Построим по регулярной грамматике КА.

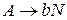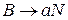1.1 Пополним грамматику правилами и , где 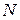- новый нетерминал.

1.2 Начальное состояние конечного автомата 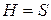. Множество состояний автомата 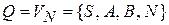, множество символов входного алфавита .

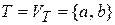1.3 Значения сформированной функции переходов даны в таблице 2.7.

Таблица 2.7 – Функция переходов автомата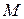

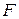	S	A	B	N
a	A, B	A	N
b		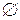N	B

1.4 Множество заключительных состояний .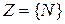

1.5 Для начального символа грамматики e-правила отсутствуют.

Конечный автомат М - недетерминированный, граф НКА представлен на рисунке 2.5.

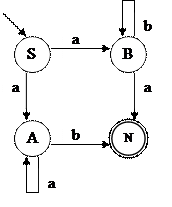Рисунок 2.5 - Граф НКА