2015-02-18
985
Алгоритм Устранение недостижимых состояний КА
Вход: КА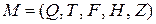 
.
Выход: КА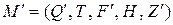 
.
Шаг 1. Поместить начальное состояние КА в список достижимых состояний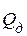 
, т.е. 
.
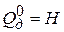Шаг 2. Для новых элементов списка достижимых состояний пополнить список группой их состояний-приемников, отсутствующих в списке, т.е.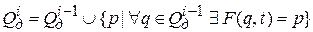 
.
Шаг 3. Повторить шаг 2, пока список достижимых состояний не перестанет меняться. То есть, если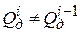 
, то i = i +1, иначе 
.
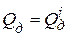Шаг 4. Исключить из множества Q состояний КА все состояния, отсутствующие в списке Qд достижимых состояний, т.е.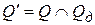 
.
Шаг 5. Исключить недостижимые заключительные состояния и функции переходов, содержащие недостижимые состояния, т.е.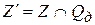 
, 
.
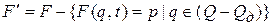Пример Устранить недостижимые состояния КА 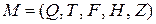, где Q = { A, B, C, D, E, F, G }, T = { a, b }, H = { A }, Z = { D, E } и функция переходов задана таблицей 2.4. Граф исходного КА М представлен на рисунке 2.3.
Таблица 2.4 – Функция переходов конечного автомата M
| F | A | B | C | D | E | F | G |
| a | B | C | B | D | F | ||
| b | C | D | E | E | D | G | E |
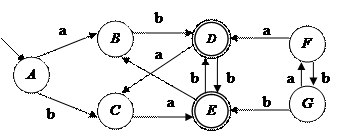
Рисунок 2.2 – Граф исходного конечного автомата М
Последовательность устранения недостижимых состояний КА имеет вид:
Q 0 = { A };
Q 1 = { A, B, C };
Q 2 = { A, B, C, D, E };
Q 3 = { A, B, C, D, E }; т.к. Q 2 = Q 3, то Q д = { A, B, C, D, E }.
Q н = { F, G };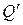 
= { A, B, C, D, E }; 
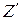= { D, E }.
Функция переходов автомата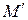 
представлена в таблице 2.6.
Таблица 2.5 - Функция переходов автомата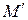
| F | A | B | C | D | E |
| a | B | C | B | ||
| b | C | D | E | E | D |
|
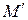после устранения недостижимых состояний представлен на рисунке 2.5.  |
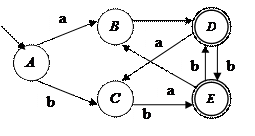Рисунок 2.3 - Граф КА 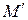после устранения недостижимых состояний
