Мода и медиана в статистике

Для характеристики структуры вариационных рядов применяются показатели особого рода, которые можно назвать структурными средними. К ним относятся мода и медиана.

Мода – это наиболее часто встречающаяся величина признака в данной совокупности.

Медианой называется такое значение варьирующего признака, которое находится в середине вариационного ряда, все варианты которого расположены в порядке возрастания или убывания значений признака.

Определить моду и медиану в дискретном вариационном ряду очень просто. Например, чтобы определить медиану, необходимо сумму частот разделить пополам и к полученному результату добавить 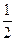, а мода определяется на глаз.

Для интервальных рядов распределения с равными интервалами мода определяется по формуле:

М_о= ,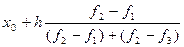

где х₀ и h – соответственно нижняя граница и ширина модального интервала, f₁, f₂, f₃ – частоты соответственно модального, предмодального и послемодального интервалов.

В интервально вариационном ряду медиана вычисляется по формуле:

М_е ,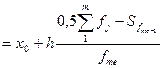

где x₀ и h – соответственно нижняя граница и ширина медианного интервала; f_j – сумма чаcтот ряда; f_me – частота медианного интервала; 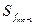- сумма накопленных частот, предшествующих медианному интервалу.