Содержание лекции. Этот метод основан на понятии о фазовом пространстве

Этот метод основан на понятии о фазовом пространстве. Известно, что

состояние системы, описываемое дифференциальным уравнением, вполне определяется, если в каждый момент времени значение регулируемой величины и её (n-1) производных известно (n – порядок дифференциального уравнения). Это даёт возможность представить состояние системы в некотором n-мерном пространстве, которое называется фазовым пространством.

Рассмотрим математическую модель системы в форме дифференциальных уравнений первого порядка, разрешенных относительно производных

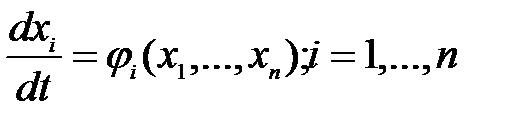. (2.1)

В правые части уравнений (11.1) время t явно не входит, такие системы называют автономными. На автономные системы не действуют внешние силы. Автономные системы стационарны ― их свойства неизменны во времени.

Состояниеконечномерной динамической системы (2.1) характеризуется вектором в n -мерном пространстве 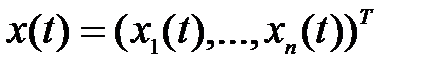. Начальное состояние x (0) автономной системы (2.1) полностью определяет ее поведение для t > 0 независимо от предыстории, т.е. того, каким путем система пришла в это состояние. Геометрическое место точек конца вектора x (t) при t ³ 0 образует траекторию состояния ― образ поведения при конкретном начальном состоянии. На рис. 2.1 иллюстрируется траектория трехмерной системы.

Рис. 2.1. Траектория изменения состояния

Хотя геометрическая интерпретация метода пространства состояний распространяется на системы любого порядка, важное его преимущество ― наглядность ― наиболее ярко проявляется в случае систем второго порядка, когда состояния системы представляются точками на фазовой плоскости. Следует добавить, что нелинейные модели второго порядка позволяют выявлять многие принципиальные особенности поведения динамических систем; это определяет методическое, теоретическое и практическое значение метода фазовой плоскости. Применение метода может быть оправданным для предварительного анализа новой системы по упрощенным моделям, поскольку метод фазовой плоскости дает наглядную картину общего характера поведения рассматриваемой динамической системы. Во второй части анализа качественные исследования, основанные на таком представлении, следует дополнить количественными, с помощью которых можно получить численные результаты, но нельзя выявить общие закономерности движения.

Метод фазовой плоскости дает возможность изобразить качественную картину всей совокупности свободных движений (процессов) для выбранной области начальных условий (состояний), а при необходимости ― провести точные исследования интересующих типов движений.

Пусть заданы уравнения системы второго порядка

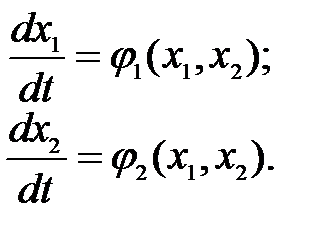(2.2)

Для получения фазовой траектории при начальных условиях x ₁₀ = x ₁(0) и x ₂₀ = x ₂(0)из решения системы (2.2)

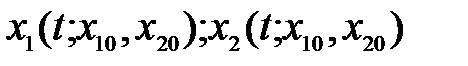(2.3)

следует исключить время t, т.е. получить зависимость

.

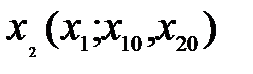На рис. 2.2 показана соответствующая графическая процедура получения фазовой траектории.

а б

Рис. 2.2. Графическая процедура построения фазовой траектории

Если изменить начальные условия, но так, что вектор начального состояния попадает на ранее построенную фазовую траекторию (точка a на рис. 2.2, б), то новая траектория совпадает со старой. Можно видеть, что отрезок фазовой траектории изображает бесчисленное множество движений при начальных состояниях системы, совпадающих с траекторией. Это упрощает вывод обобщающих суждений о свойствах системы по совокупностям фазовых траекторий ― фазовому портрету динамической системы.

В случае автономности динамических систем время t явно не входит в правую часть дифференциальных уравнений (2.2). Рассматривая координату x ₁ как независимую переменную, можно путем деления второго уравнения системы (11.2) на первое исключить время и получить одно дифференциальное уравнение первого порядка

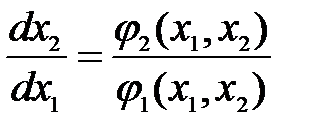. (2.4)

Решая это уравнение при конкретных начальных условиях, можно получить фазовые траектории.

Если функции j₁ 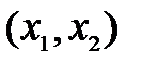и j₂ 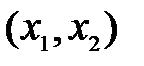однозначны, то каждой точке 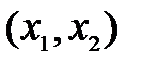соответствует единственное значение производной dx ₂/ dx ₁ (наклона касательной к фазовой траектории), т.е. через эту точку фазовой плоскости проходит только одна фазовая траектории. Единственность нарушается в так называемых особых точках, соответствующих состояниям равновесия системы:

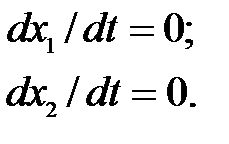(2.5)

Координаты особых точек определяются из уравнений

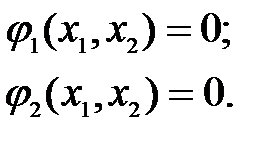(2.6)

В особых точках, как это следует из (2.4) и (2.5), имеется неопределенность производной: dx ₂/ dx ₁=0/0. Каждая особая точка изображает отдельное (тривиальное) решение системы (2.2) и должна рассматриваться как отдельная фазовая траектория.

В качестве фазовой переменной x ₁, как правило, выбирается переменная на входе нелинейного элемента x.

Переменная x ₂ обычно выбирается из условия x ₂ = dx / dt = x¢. В этом случае система уравнений (11.2) примет вид:

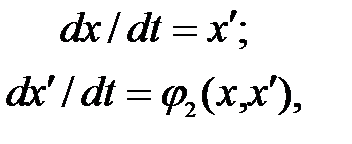(2.7)

а вместо (2.4) имеем:

. (2.8)

Выполнение условия x ₂ = dx / dt придает фазовой плоскости следующие свойства:

- особые точки располагаются только на оси абсцисс, где x ₂ = dx / dt = 0;

- в верхней полуплоскости (x ₂ = dx / dt > 0) фазовые траектории направлены слева направо, т.е. в сторону увеличения x ₁, а в нижней полуплоскости ― справа налево;

- фазовые траектории ортогональны оси абсцисс, так как из (2.8) при x ₂ = 0 следует dx ₂/ dv ₁ = ¥.

Контрольные вопросы для самоподготовки

1. Что называется фазовым пространством?

2. Что показывает фазовая траектория движения системы?

3. Что называется особой точкой фазовой траектории?

4. Что называется фазовой плоскостью?

5. Что называется фазовым портретом?

6. Где располагается особая точка на фазовом пространстве?