Рассмотрим двумерную дискретную случайную величину 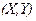 . Допустим, что в результате опыта составляющая
. Допустим, что в результате опыта составляющая 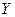 приняла значение
приняла значение 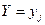 . При этом составляющая
. При этом составляющая 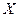 может принять одно из возможных значений
может принять одно из возможных значений 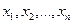 .
.
Обозначим условную вероятность того, что случайная величина примет значение 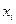 при условии, что составляющая
при условии, что составляющая 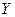 приняла значение
приняла значение 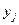 через
через 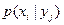 .
.
Условным распределением составляющей 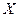 при условии, что
при условии, что 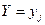 , называется совокупность вероятностей
, называется совокупность вероятностей 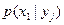 ,
, 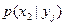 ,...,
,..., 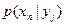 , вычисленных в предположении, что событие
, вычисленных в предположении, что событие 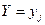 наступило.
наступило.
Зная закон распределения двумерной дискретной случайной величины, можно вычислить условные законы распределения составляющих:
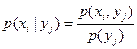 ,
,
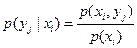 .
.
Пример 1. Двумерная случайная величина задана таблицей распределения:
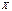 | 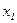 | 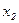 | 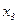 | |
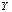 | ||||
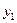 | 0,1 | 0,3 | 0,2 | |
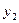 | 0,06 | 0,18 | 0,16 |
Записать закон распределения составляющей 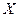 при
при 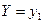 .
.
Решение. Рассчитаем условные вероятности:
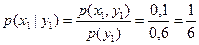 ,
,
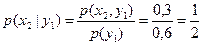 ,
,
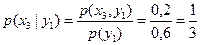 .
.
 2015-02-24
2015-02-24 704
704







