Условной плотностью распределения 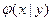 составляющей
составляющей 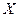 при данном значении
при данном значении 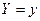 называется функция
называется функция
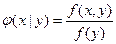 ,
,
где 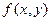 - плотность распределения системы случайных величин,
- плотность распределения системы случайных величин,
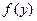 - плотность распределения составляющей
- плотность распределения составляющей 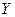 .
.
Если известна плотность совместного распределения, то условные плотности составляющих могут быть найдены по формулам:
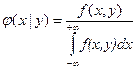 ,
, 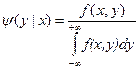 .
.
Пример 2. Плотность совместного распределения системы двух непрерывных случайных величин задана формулой
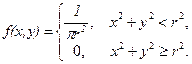
Найти условную плотность вероятности 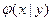 .
.
Решение. Используем вышеприведенную формулу
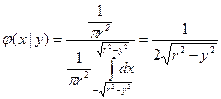 при
при 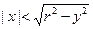 .
.
Так как 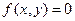 при
при 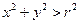 , то
, то 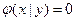 при
при 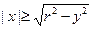 .
.
 2015-02-24
2015-02-24 417
417







