Условным математическим ожиданием дискретной случайной величины 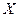 при
при 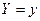 называется число
называется число
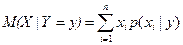 .
.
Для непрерывных случайных величин условное математическое ожидание определяется интегралом
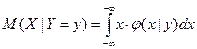
Условное математическое ожидание называют также регрессией 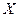 на
на 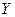 .
.
Корреляционным моментом случайных величин 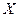 и
и 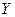 называется математическое ожидание произведения отклонений этих величин от их математических ожиданий
называется математическое ожидание произведения отклонений этих величин от их математических ожиданий
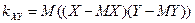 .
.
Коэффициентом корреляции называется
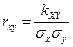 .
.
Линейной средней квадратической регрессией 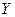 на
на 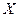 называется функция вида
называется функция вида
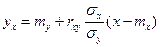 ,
,
где 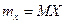 ,
, 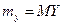 ,
, 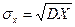 ,
, 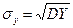 .
.
 2015-02-24
2015-02-24 372
372








