Вопросы и задания к главе 9

8.9 Дополнительная литература к главе 9.

1. Романов, В.П. Интеллектуальные информационные системы в экономике / В.П. Романов. - М.: Экзамен, 2003. - 496 с.

2. Хайкин С. Нейронные сети: полный курс: 2 изд. / пер. с англ. - М.-СПб.-Киев: Вильямс, 2008. - 1104 с.

3. Барский А.Б. Нейронные сети: распознавание, управление, принятие решений. - М.: Финансы и статистика, 2004. - 176 с. - (Прикладные информационные технологии).

4. Нейронные сети: Метод. указания к самостоятельным и лаб. работам: Дисц. "Логическое программирование и экспертные системы": Спец. 22.01, 4 курс д/о / Вятский гос. техн. ун-т, Фак. автоматики и вычислительной техники, Каф. электронных вычислительных машин; Сост. В.С. Ростовцев; Рец. В.У. Сысоев. - Киров: ВятГТУ, 1999. - 34 с.

5. Решение задач искусственного интеллекта при помощи нейронных сетей: лаб. практикум: дисц. "Интеллект. информ. системы": спец. 07.19.00, 3 курс, д/о / Федер. агентство по образованию, ГОУ высш. проф. образования Вят. гос. ун-т, фак. автоматики и вычислит. техники, каф. автоматики и телемеханики; [сост. Ю. В. Ланских; рец. А. Н. Рапопорт]. - Киров: ВятГУ, 2004. - 16 с.

6. Боровиков В.П., Ивченко Г.И. Прогнозирование в системе Statistica в среде Windows. Основы теории и интенсивная практика на компьютере. - М.: Финансы и статистика, 1999. - 379 с.

ПРИЛОЖЕНИЕ 1. Таблица интегральной функции нормального распределения S(x), симметричной относительно среднего и выражающей заштрихованную площадь на графике при 0 < x < 2,89: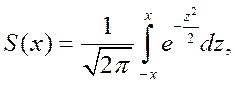

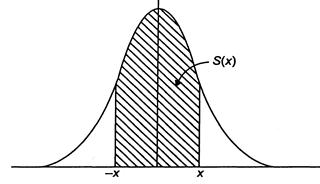
Её можно представить как разность интегральных функций S(x) = F_X - F_-X (Целые части и десятые доли х - в крайнем левом столбце; сотые доли х - в верхней строке).


0,0	0,0000	0,0080	0,0160	0,0239	0,0319	0,0399	0,0478	0,0558	0,0638	0,0717
0,1	0,0797	0,0876	0,0955	0,1034	0,1113	0,1192	0,1271	0,1350	0,1428	0,1507
0,2	0,1585	0,1663	0,1741	0,1819	0,1897	0,1974	0,2051	0,2128	0,2205	0,2282
0,3	0,2358	0,2434	0,2510	0,2586	0,2661	0,2737	0,2812	0,2886	0,2960	0,3035
0,4	0,3108	0,3182	0,3255	0,3328	0,3401	0,3473	0,3545	0,3616	0,3688	0,3759
0,5	0,3829	0,3899	0,3969	0,4039	0,4108	0,4177	0,4245	0,4313	0,4381	0,4448
0,6	0,4515	0,4581	0,4647	0,4713	0,4778	0,4843	0,4907	0,4971	0,5035	0,5098
0,7	0,5161	0,5223	0,5285	0,5346	0,5407	0,5467	0,5527	0,5587	0,5646	0,5705
0,8	0,5763	0,5821	0,5878	0,5935	0,5991	0,6047	0,6102	0,6157	0,6211	0,6265
0,9	0,6319	0,6372	0,6424	0,6476	0,6528	0,6579	0,6629	0,6679	0,6729	0,6778
1,0	0,6827	0,6875	0,6923	0,6970	0,7017	0,7063	0,7109	0,7154	0,7199	0,7243
1,1	0,7287	0,7330	0,7373	0,7415	0,7457	0,7499	0,7540	0,7580	0,7620	0,7660
1,2	0,7699	0,7737	0,7775	0,7813	0,7850	0,7887	0,7923	0,7959	0,7994	0,8029
1,3	0,8064	0,8098	0,8132	0,8165	0,8198	0,8230	0,8262	0,8293	0,8324	0,8355
1,4	0,8385	0,8415	0,8444	0,8473	0,8501	0,8529	0,8557	0,8584	0,8611	0,8638
1,5	0,8664	0,8690	0,8715	0,8740	0,8764	0,8789	0,8812	0,8836	0,8859	0,8882
1,6	0,8904	0,8926	0,8948	0,8969	0,8990	0,9011	0,9031	0,9051	0,9070	0,9090
1,7	0,9109	0,9127	0,9146	0,9164	0,9181	0,9199	0,9216	0,9233	0,9249	0,9265
1,8	0,9281	0,9297	0,9312	0,9327	0,9342	0,9357	0,9371	0,9385	0,9399	0,9412
1,9	0,9426	0,9439	0,9451	0,9464	0,9476	0,9488	0,9500	0,9512	0,9523	0,9534
2,0	0,9545	0,9556	0,9566	0,9576	0,9586	0,9596	0,9606	0,9616	0,9625	0,9634
2,1	0,9643	0,9651	0,9660	0,9668	0,9676	0,9684	0,9692	0,9700	0,9707	0,9715
2,2	0,9722	0,9729	0,9736	0,9743	0,9749	0,9756	0,9762	0,9768	0,9774	0,9780
2,3	0,9786	0,9791	0,9797	0,9802	0,9807	0,9812	0,9817	0,9822	0,9827	0,9832
2,4	0,9836	0,9841	0,9845	0,9849	0,9853	0,9857	0,9861	0,9865	0,9869	0,9872
2,5	0,9876	0,9879	0,9883	0,9886	0,9889	0,9892	0,9895	0,9898	0,9901	0,9904
2,6	0,9907	0,9910	0,9912	0,9915	0,9917	0,9920	0,9922	0,9924	0,9926	0,9928
2,7	0,9931	0,9933	0,9935	0,9937	0,9939	0,9940	0,9942	0,9944	0,9946	0,9947
2,8	0,9949	0,9951	0,9952	0,9953	0,9955	0,9956	0,9958	0,9959	0,9960	0,9961

ПРИЛОЖЕНИЕ 2. Значения t- распределения (критерий Стьюдента)

f	Уровень значимости α
0,5	0,25	0,1	0,05	0,025	0,01	0,005	0,001
	1,00	2,41	6,31	12,7	25,5	63,7
	1,816	1,60	2,92	4,30	6,21	9,92	14,1	31,6
	1,765	1,42	2,35	3,18	4,18	5,84	7,45	12,9
	1,741	1,34	2,13	2,78	3,50	4,60	5,60	8,61
	1,727	1,30	2,01	2,57	3,16	4,03	4,77	6,86
	1,718	1,27	1,94	2,45	2,97	3,71	4,32	5,96
	1,711	1,25	1,89	2,36	2,84	3,50	4,03	5,40
	1,706	1,24	1,86	2,31	2,75	3,36	3,83	5,04
	1,703	1,23	1,83	2,26	2,68	3,25	3,69	4,78
	1,700	1,22	1,81	2,23	2,63	3,17	3,58	4,59
	1,697	1,21	1,80	2,20	2,59	3,11	3,50	4,44
	1,695	1,21	1,78	2,18	2,56	3,05	3,43	4,32
	1,694	1,20	1,77	2,16	2,53	3,01	3,37	4,22
	1,692	1,20	1,76	2,14	2,51	2,98	3,33	4,14
	1,691	1,20	1,75	2,13	2,49	2,95	3,29	4,07
	1,690	1,19	1,75	2,12	2,47	2,92	3,25	4,01
	1,689	1,19	1,74	2,11	2,46	2,90	3,22	3,96
	1,688	1,19	1,73	2,10	2,44	2,88	3,20	3,92
	1,688	1,19	1,73	2,09	2,43	2,86	3,17	3,88
	1,687	1,18	1,72	2,09	2,42	2,85	3,15	3,85
	1,686	1,18	1,72	2,08	2,41	2,83	3,14	3,82
	1,686	1,18	1,72	2,07	2,41	2,82	3,12	3,79
	1,685	1,18	1,71	2,07	2,40	2,81	3,10	3,77
	1,685	1,18	1,71	2,06	2,39	2,80	3,09	3,74
	1,684	1,18	1,71	2,06	2,38	2,79	3,08	3,72
	1,684	1,18	1,71	2,06	2,38	2,78	3,07	3,71
	1,684	1,18	1,70	2,05	2,37	2J7	3,06	3,69
	1,683	1,17	1,70	2,05	2,37	2,76	3,05	3,67
	1,683	1Д7	1,70	2,05	2,36	2,76	3,04	3,66
	1,683	1,17	1,70	2,04	2,36	2,75	3,03	3,65
	1,681	1,17	1,68	2,02	2,33	2,70	2,97	3,55
	1,679	1,16	1,67	2,00	2,30	2,66	2,91	3,46
	1,677	1,16	1,66	1,98	2,27	2,62	2,86	3,37
∞	1,674	1,15	1,64	1,96	2,24	2,58	2,81	3,29

ПРИЛОЖЕНИЕ.. Коэффициенты Диксона, учитывающие экстремальные значения при заданных значениях уровня значимости α

Обозначение коэффициента Диксона	Число наблюдений n	α
	0,1	0,05	0,01	0,005
r₁₀		0,886	0,941	0,988	0,994
	0,679	0,765	0,889	0,926
	0,557	0,642	0,78	0,821
	0,482	0,56	0,698	0,74
	0,434	0,507	0,637	0,68
r₁₁		0,479	0,554	0,683	0,725
	0,441	0,512	0,635	0,677
	0,409	0,477	0,597	0,639
r₂₀		0,935	0,967	0,992	0,996
	0,782	0,845	0,929	0,95
	0,67	0,736	0,836	0,865
	0,596	0,661	0,778	0,814
	0,545	0,607	0,71	0,746
	0,505	0,565	0,667	0,7
	0,474	0,531	0,632	0,664
r₂₁		0,517	0,576	0,679	0,713
	0,49	0,546	0,642	0,675
	0,467	0,521	0,615	0,649
r₂₂		0,492	0,546	0,641	0,674
	0,472	0,525	0,616	0,647
	0,454	0,507	0,595	0,624
	0,438	0,49	0,577	0,605
	0,424	0,475	0,561	0,589
	0,412	0,462	0,547	0,575
	0,401	0,45	0,535	0,562
	0,391	0,44	0,524	0,551
	0,382	0,43	0,514	0,541
	0,374	0,421	0,005	0,532
	0,367	0,413	0,497	0,524
	0,36	0,406	0,489	0,516
	0,354	0,399	0,486	0,508
	0,348	0,393	0,475	0,501
	0,342	0,387	0,469	0,495
	0,337	0,381	0,463	0,489
	0,332	0,376	0,457	0,483

ПРИЛОЖЕНИЕ.. Значения F_KP для уровня значимости α = 0,05

f₂						f₁
										∞
	161,45	199,50	215,72	224,57	230,17	233,97	238,89	243,91	249,04	254,32
	18,51	19,00	19,16	19,25	19,30	19,33	19,37	19,41	19,45	19,50
	10,13	9,55	9,28	9,12	9,01	8,94	8,84	8,74	8,64	8,53
	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,77	5,63
	6,61	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,53	4,36
	5,99	5,14	4,76	4,53	4,39	4,28	4,15	4,00	3,84	3,67
	5,59	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,41	3,23
	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,12	2,93
	5,12	4,26	4,86	3,63	3,48	3,37	3,23	3,07	2,90	2,71
	4,96	4,10	3,71	3,48	3,33	3,22	3,07	2,91	2,74	2,54
	4,84	3,98	3,59	3,36	3,20	3,09	2,95	2,79	2,61	2,40
	4,75	3,88	3,49	3,26	3,11	3,00	2,85	2,69	2,50	2,30
	4,67	3,80	3,41	3,18	3,02	2,92	2,77	2,60	2,42	2,21
	4,60	3,74	3,34	3,11	2,96	2,85	2,70	2,53	2,35	2,13
	4,54	3,68	3,29	3,06	2,90	2,79	2,64	2,48	2,29	2,07
	4,49	3,63	3,24	3,01	2,85	2,74	2,59	2,42	2,24	2,01
	4,41	3,55	3,16	2,93	2,77	2,66	2,51	2,34	2,15	1,92
	4,35	3,49	3,10	2,87	2,71	2,60	2,45	2,28	2,08	1,84
	4,32	3,47	3,07	2,84	2,68	2,57	2,42	2,25	2,05	1,81
	4,30	3,44	3,05	2,82	2,66	2,55	2,40	2,23	2,03	1,78
	4,28	3,42	3,03	2,80	2,64	2,53	3,38	2,20	2,00	1,76
	4,26	3,40	3,01	2,78	2,62	2,51	2,36	2,18	1,98	1,73
	4,24	3,38	2,99	2,76	2,60	2,49	2,34	2,16	1,96	1,71
	4,22	3,37	2,98	2,74	2,59	2,47	2,32	2,15	1,95	1,69
	4,21	3,35	2,96	2,73	2,57	2,46	2,30	2,13	1,93	1,67
	4,20	3,34	2,35	2,71	2,56	2,44	2,29	2,12	1,91	1,65
	4,17	3,32	2,92	2,69	2,53	2,42	2,27	2,09	1,89	1,62
	4,08	3,23	2,84	2,61	2,45	2,34	2,18	2,00	1,79	1,52
	4,03	3,18	2,79	2,56	2,40	2,29	2,13	1,95	1,74	1,44
	4,00	3,15	2,76	2,52	2,37	2,25	2,10	1,92	1,70	1,39
	3,98	3,13	2,74	2,50	2,35	2,23	2,07	1,89	1,67	1,35
	3,96	3,11	2,72	2,49	2,33	2,21	2,06	1,88	1,65	1,31
	3,95	3,10	2,71	2,47	2,32	2,20	2,04	1,86	1,64	1,28
	3,94	3,09	2,70	2,46	2,30	2,19	2,03	1,85	1,63	1,26
	3,92	3,07	2,68	2,44	2,29	2,17	2,01	1,83	1,60	1,21
	3,90	3,06	2,66	2,43	2,27	2,16	2,00	1,82	1,59	1,18
	3,89	3,04	2,65	2,42	2,26	2,14	1,98	1,80	1,57	1,14
	3,87	3,03	2,64	2,41	2,25	2,13	1,97	1,79	1,55	1,10
	3,86	3,02	2,63	2,40	2,24	2,12	1,96	1,78	1,54	1,07
	3,86	3,01	2,62	2,39	2,23	2,11	1,96	1,77	1,54	1,06
	3,85	3,00	2,61	2,38	2,22	2,10	1,95	1,76	1,53	1,03
∞	3,84	2,99	2,60	2,37	2,21	2,09	1,94	1,75	1,52	1,00

ПРИЛОЖЕНИЕ. Значения критерия Кохрана G_kp для N выборок, каждая из которых состоит из n параллельных опытов (или контрольных замеров), при заданных значениях коэффициента риска (уровня значимости) α =0,05 и α =0,01 (при N=∞ G_kp=1 для всех значений n; при n=∞ G_kp=1/N)

N	n

0,05	0,01	0,05	0,01	0,05	0,01	0,05	0,01	0,05	0,01	0,05	0,01	0,05	0,01	0,05	0,01	0,05	0,01
	*	*	0,97	0,99	0,94	0,98	0,91	0,96	0,88	0,94	0,85	0,92	0,83	0,90	0,82	0,88	0,80	0,87
	0,97	0,99	0,87	0,94	0,80	0,88	0,75	0,83	0,71	0,79	0,68	0,76	0,65	0,73	0,63	0,71	0,62	0,69
	0,91	0,97	0,77	0,86	0,68	0,78	0,63	0,72	0,59	0,68	0,56	0,64	0,54	0,61	0,52	0,59	0,50	0,57
	0,84	0,93	0,68	0,79	0,60	0,70	0,54	0,63	0,51	0,59	0,48	0,55	0,46	0,53	0,44	0,50	0,42	0,49
	0,78	0,88	0,62	0,72	0,53	0,65	0,48	0,56	0,44	0,52	0,42	0,49	0,40	0,46	0,38	0,44	0,37	0,42
	0,73	0,84	0,56	0,66	0,48	0,57	0,43	0,51	0,40	0,47	0,37	0,43	0,35	0,41	0,34	0,39	0,33	0,38
	0,68	0,79	0,52	0,62	0,44	0,52	0,39	0,46	0,36	0,42	0,34	0,39	0,32	0,37	0,30	0,35	0,29	0,34
	0,64	0,75	0,48	0,57	0,40	0,48	0,36	0,43	0,33	0,39	0,31	0,36	0,29	0,34	0,28	0,32	0,27	0,31
	0,60	0,72	0,44	0,54	0,37	0,45	0,33	0,39	0,30	0,36	0,28	0,33	0,27	0,31	0,25	0,29	0,24	0,28
	0,54	0,65	0,39	0,48	0,33	0,39	0,29	0,34	0,26	0,31	0,24	0,29	0,23	0,27	0,22	0,25	0,21	0,24
	0,47	0,57	0,33	0,41	0,28	0,33	0,24	0,39	0,22	0,26	0,20	0,24	0,19	0,22	0,18	0,21	0,17	0,20
	0,39	0,48	0,27	0,33	0,22	0,27	0,19	0,23	0,17	0,20	0,16	0,19	0,15	0,17	0,14	0,16	0,14	0,16
	0,34	0,42	0,24	0,29	0,19	0,23	0,17	0,20	0,15	0,18	0,14	0,16	0,13	0,15	0,12	0,14	0,12	0,13
	0,29	0,36	0,20	0,24	0,16	0,19	0,14	0,16	0,12	0,15	0,11	0,13	0,11	0,12	0,10	0,12	0,10	0,11
	0,24	0,29	0,16	0,19	0,13	0,15	0,11	0,13	0,10	0,11	0,09	0,10	0,08	0,10	0,08	0,09	0,07	0,09
	0,17	0,22	0,11	0,14	0,09	0,11	0,08	0,09	0,07	0,08	0,06	0,07	0,05	0,07	0,06	0,06	0,05	0,06
	0,10	0,12	0,06	0,08	0,05	0,06	0,04	0,05	0,04	0,04	0,03	0,04	0,03	0,04	0,03	0,03	0,03	0,03

* G_kp = 0,995

Литература:

7. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высш. образование, 2008. - 479 с.

8. Вентцель, Е.С. Теория вероятностей и ее инженерные приложения: учеб. пособие для втузов / Е.С. Вентцель, Л.А. Овчаров. - 4-е изд., стер. - М.: Высш. шк., 2007. - 491 с.

9. Теория статистики / Под ред. Р.А. Шмойловой. - 2-е изд., доп. и перераб. - М.: Финансы и статистика, 2009. - 655 с.

10. Сиденко, А.В. Статистика / А.В. Сиденко, Г.Ю. Попов. - М.: Дело и Сервис, 2000. - 464 с.

11. Орлов А.И. Прикладная статистика: учебник для вузов. - М.: Экзамен, 2004. - 656 с.

12. Орлов А.И. Эконометрика. Учебник для вузов. Изд. 2-е, исправленное и дополненное. - М.: Изд-во "Экзамен", 2003. – 576 с.

13. Айвазян С. А., Методы эконометрики. учебник для вузов по спец. "Математические методы в экономике" и др. экон. спец. - 2010. - 506 с.

14. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. - М.: ФИЗМАТЛИТ, 2006. - 816 с.

15. Натан, А.А. Математическая статистика / А.А. Натан, О.Г. Горбачев, С.А. Гуз. - М.: МЗ Пресс, 2005. - 160 с.

16. Математическая статистика / В.Б. Горяинов, И.В. Павлов, Г.М. Цветкова и др.; под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. - 424 с. - (Сер. Математика в техническом университете. Вып. XVII).

17. Шведов, А.С.Теория вероятностей и математическая статистика [Текст]: учеб. пособие для вузов / А.С. Шведов; Гос. ун-т — Высшая школа экономики. — 2-е изд., перераб. и доп. — М: Изд. дом ГУ ВШЭ, 2005. — 254, [I, II] с. — (Учебники Высшей школы экономики). — Литерат.: с. 247—249.

18. Палий, И.А. Прикладная статистика: учеб. пособие для вузов / Ирина Абрамовна Палий. - М.: Дашков и К⁰: Наука Спектр, 2008. - 223 с.

19. Вуколов Э.А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXCEL. - М.: ФОРУМ; ИНФРА-М, 2004. - 464 с. - (Профессиональное образование).

20. Рогов, Владимир Александрович Методика и практика технических экспериментов: учеб. пособие для вузов по напр. подготовки бакалавров и магистров "Технология, оборудование и автоматизация машиностроительных производств" и по напр. подготовки дипломированных спец. "Конструкторско-технологическое обеспечение машиностроит. производств" / В.А. Рогов, Г.Г. Позняк. - М.: Академия, 2005. - 283 с.

21. Современный эксперимент: подготовка, проведение, анализ результатов / В.Г. Блохин, О.П. Глудкин, А.И. Гуров, М.А. Ханин; под ред. О.П. Глудкина. - М.: Радио и связь, 1997. - 232 с.

22. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере / под ред. В.Э. Фигурнова. - М.: ИНФРА-М, 2008.. - 528 с.

23. Клячкин В.Н. Статистические методы в управлении качеством: компьютерные технологии. - М.: Финансы и статистика, 2007. - 304 с.

24. Козлов А.Ю., Шишов В.Ф. Пакет анализа MS Ехсеl в экономико-статистических расчётах. - М.: ЮНИТИ-ДАНА, 2003. - 139 с.

25. Козлов А.Ю., Мхитарян В.С., Шишов В.Ф. Статистические функции MS Excel в экономико-статистических расчетах / под ред. В.С. Мхитаряна. - М.: ЮНИТИ-ДАНА, 2003. - 231 с.

26. Макарова Н.В., Трофимец В.Я. Статистика в Ехсеl. - М.: Финансы и статистика, 2002. — 368 с.

27. Зарубин В.С. Математическое моделирование в технике: учебник для вузов / под ред. В.С. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. - 496 с. (Сер. Математика в техническом университете. Вып. XXI, заключительный).

28. Ивченко Г.И., Медведев Ю.И. Математическая статистика: учеб. пособ. для втузов. - 2-е изд., доп. - М.: Высш. шк., 1992. - 304 с.

29. Ниворожкина Л.И., Арженовский С.В. Многомерные статистические методы в экономике: учебник. - М.: Издательско-торговая корпорация «Дашков и К°»; Ростов н/Д: Наука-Спектр, 2008. - 224 с.

30. ГОСТ Р ИСO 9001 - 2001. Системы менеджмента качества. Требования. - Введ. 2001-08-31. - М.: Госстандарт России, 2001. - 20 с.

31. ГОСТ Р ИСО/ТО 10017-2005. Статистические методы. Руководство по применению в соответствии с ГОСТ Р ИСО 9001. - Дата введения 2005-07-01. - М.: Стандартинформ, 2005. - 19 с.

32. ГОСТ 16504-81. Система государственных испытаний продукции. Испытания и контроль качества продукции. Основные термины и определения. - Взамен ГОСТ 16504-74; Введ. 01.01.82. - М.: Изд-во стандартов, 1982. - 28 с.

33. ГОСТ Р ИСО 5725-1-2002.Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения. - Введ. 2002-11-01. - М.: ИПК Издательство стандартов, 2002. - 30 с.

34. ГОСТ Р ИСО 9004-2001. Системы менеджмента качества. Рекомендации по улучшению деятельности. - М.: Госстандарт России, 2005. - 47 с.

35. Александровская Л.Н. Современные методы обеспечения безотказности сложных технических систем / Л.Н. Александровская, А.П. Афанасьев, А.А. Лисов. - М: Логос, 2001. - 208 с.

36. Острейковский В.А. Теория надежности. — М.: Высшая школа, 2003. - 463 с.

37. Строителев В.Н. Статистические методы в управлении качеством / В.Н. Строителев, В.Е. Яницкий. - М.: Европейский центр по качеству, 2002. - 164 с.

38. ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ Учебник / Под редакцией доктора экономических наук, профессора, академика М.Г. Назарова. Москва, 2010 (Сер. "Высшее экономическое образование") Политех

39. Нив, Генри Р. Пространство доктора Деминга: в 2 кн. / пер. с англ. Ю. П. Адлера, В. Л. Шпера; общ. ред. Ю. П. Адлера. - М.: Стандарты и качество, 2003. - 151 с. - Библиотека Всероссийской организации качества. - 5-94938-013-4, 4000.

40. Фаддеев, Михаил Андреевич Элементарная обработка результатов эксперимента: учеб. пособие. - СПб.: Лань, 2008. - 128 с.: ил.. - Учебники для вузов. Специальная литература. - 978-5-8114-0817-7, 2000.

41. Чурилова Э.Ю. Использование системы компьютерной обработки данных STATISTICA в преподавании статистических дисциплин // Вопросы статистики. - 2003. - № 4. - С. 42-43.