-> А-да, В-нет
А- да, В- да
А- нет, В- да
А- нет, В- нет
Даны множества: А = {–1, 2, 5, 6} и В = {–3, 2, 5, 6}. Разностью множеств В и А является множество: (набрать число)
-> -3
Первый член арифметической прогрессии равен 3, пятый -11. Разность этой прогрессии равна …. (наберите число)
-> 2
Производная 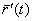 векторной функции
векторной функции 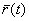 при
при 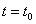 направлена по
направлена по
-> касательной прямой к годографу функции 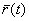 , проведенной в точке
, проведенной в точке 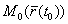
касательной прямой
касательной прямой в точке 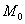
нормали к линии
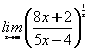 равен (наберите число)
равен (наберите число)
-> 1
Если теорема 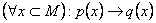 верна, то
верна, то
-> условие р(х) – достаточное условие для заключения q(x)
-> заключение q(x) – необходимое условие для р(х)
q(x) – необходимое и достаточное условие для р(х)
р(х) – необходимое и достаточное условие для q(x)
Для функции 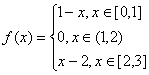
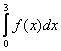 равен
равен
-> 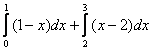
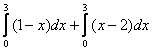
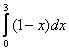
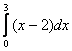
Установите соответствие между названием разрыва функции y = f(x0) в точке x0 и его определением
-> устранимый разрыв <-> 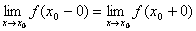 , f(x0) не существует
, f(x0) не существует
-> неустранимый разрыв I рода <-> 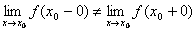
-> разрыв II рода <-> нет конечных пределов слева или справа
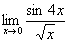 равен (наберите число)
равен (наберите число)
-> 0
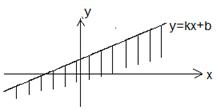
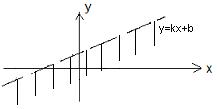
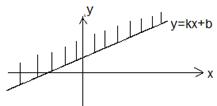
Множество А = 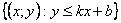 изображено на чертеже
изображено на чертеже
-> 
Общее решение дифференциального уравнения 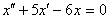 имеет вид
имеет вид
-> 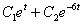
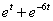
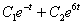
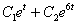
Уравнение 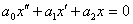 имеет фундаментальную систему решений
имеет фундаментальную систему решений 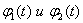 . Общее решение имеет вид
. Общее решение имеет вид
-> 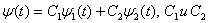 – произвольные постоянные
– произвольные постоянные
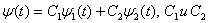 – переменные
– переменные
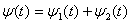
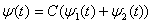
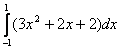 равен (набрать число)
равен (набрать число)
-> 6
Дифференциальное уравнение 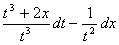 = 0 является уравнением
= 0 является уравнением
-> с полным дифференциалом
однородным первого порядка
Бернулли
с разделяющимися переменными
Укажите соответствие между условием и заключением
-> если 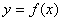 возрастает на интервале (a, b) <-> то тангенс угла наклона касательной к графику
возрастает на интервале (a, b) <-> то тангенс угла наклона касательной к графику 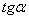 > 0
> 0
-> если 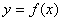 убывает на интервале (a,b) <-> то тангенс угла наклона касательной к графику
убывает на интервале (a,b) <-> то тангенс угла наклона касательной к графику 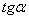 < 0
< 0
-> если в точке с абсциссой x0 функция имеет экстремум <-> то тангенс угла наклона касательной к графику 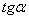 = 0
= 0
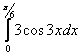 равен (набрать число)
равен (набрать число)
-> 1
Определитель Вронского для дифференциального уравнения 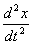 + 9x = 0 равен
+ 9x = 0 равен
-> c
ce3t
ce-3t
ce6t
Объем тела, образованного вращением вокруг оси 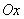 фигуры, ограниченной параболой
фигуры, ограниченной параболой 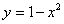 и осью
и осью 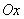 , вычисляется с помощью интеграла
, вычисляется с помощью интеграла
-> 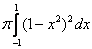

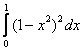
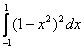
Подберите правильный ответ. -> А-да, В-нет А- да, В- да А- нет, В- да А- нет, В- нет Даны множества: А = {–1, 2, 5, 6} и В = {–3
|
|

Сейчас читают про:
 2015-03-22
2015-03-22 499
499







