Любое возвратное уравнение нечетной степени сводится к квадратному уравнению четной степени, т.к у любого возвратного уравнения нечетной степени один из корней всегда равен –1
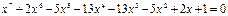
Очевидно 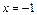 - корень уравнения.
- корень уравнения.
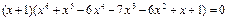
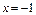 или
или 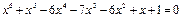
т.к 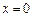 - не является корнем уравнения, то разделим обе части уравнения на
- не является корнем уравнения, то разделим обе части уравнения на 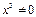
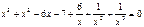
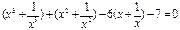
Введем замену: Пусть 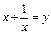 ,
, 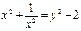 ,
, 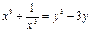
II) Уравнения вида 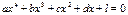 , где
, где 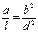 решаются как возвратные.
решаются как возвратные.
III) В следующих уравнениях используется “идея однородности”.
Пример №1.
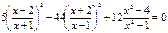
Введем замену: Пусть 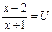 ,
, 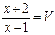 , тогда
, тогда
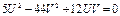
1) если 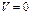 , тогда
, тогда 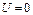 , тогда
, тогда 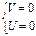
2) Разделим обе части уравнения на 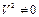 , получим
, получим
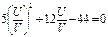
 2015-03-22
2015-03-22 774
774








