Однородное уравнение – это уравнение, в котором каждое слагаемое имеет одну и туже степень.
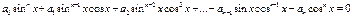 , где
, где 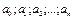 - действительные числа.
- действительные числа. 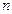 - показатель однородности.
- показатель однородности.
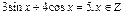
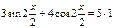
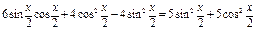
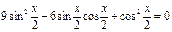
Если 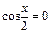 , то и
, то и 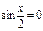 , что противоречит основному тригонометрическому тождеству, значит
, что противоречит основному тригонометрическому тождеству, значит 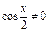 . Разделим обе части на
. Разделим обе части на 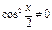 , получим:
, получим: 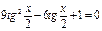
II) Уравнения вида 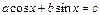
1) если 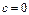 , то уравнение однородное.
, то уравнение однородное.
2) если 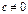 и
и 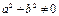 (то есть хотя бы одно из чисел
(то есть хотя бы одно из чисел 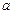 или
или 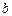 не равно 0), то разделим обе части уравнения на
не равно 0), то разделим обе части уравнения на 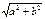 , получим
, получим
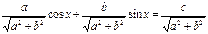
Т. к. 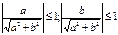 и
и 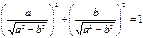 , то существует такой угол
, то существует такой угол 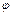 , что
, что 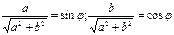 , тогда
, тогда
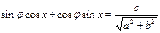
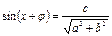
а) если, 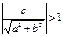 т. е.
т. е. 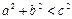 , то корней нет.
, то корней нет.
в) если, 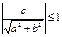 т. е.
т. е. 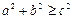 , тогда
, тогда
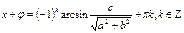
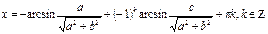
III) Решение тригонометрических уравнений с помощью замены неизвестного.
Уравнение вида 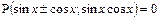 решается следующей заменой
решается следующей заменой 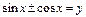 ,
, 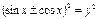 ,
, 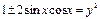 ,
, 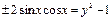
 2015-03-22
2015-03-22 692
692








