Коэффициенты теплопроводности некоторых веществ

Вещество	l, Вт/м/К	Вещество	l, Вт/м/К
Серебро		Кирпич изоляционный	0,14
Медь		Асбест листовой	0,12
Алюминий		Шлаковая вата	0,07
Латунь		Аммиак	0,570
Чугун		Вода	0,547
Накипь котельная	1,3…3,1	Воздух	0,024
Бетон	1,28	Углекислый газ	0,017

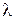Коэффициент , как и 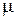, зависит от вида газа и температуры. При увеличении температуры 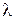растет. При высоких температурах коэффициент теплопроводности реального газа .

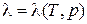Рассмотрим процесс переноса тепла с точки зрения молекулярно-кинети-ческой теории (рис. 1.3). Количество тепла, переносимое единицей массы, равно 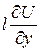, где U – внутренняя энергия единицы массы газа.

Масса молекул, пересекающих при своем движении поверхность с единичной площадью, равна 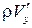, где 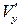– собственная скорость молекул, т. е. через единичную площадку в единицу времени переносится энергия (количество тепла), равная

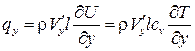, (1.6)

так как 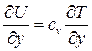. Сравнивая формулы (1.5) и (1.6), можно сделать вывод, что 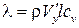. Таким образом, коэффициент l пропорционален скорости хаотического движения молекул, являющейся функцией температуры газа, поэтому .

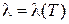При температурах до 2 000 К коэффициент теплопроводности можно определить через коэффициент динамической вязкости по следующей формуле:

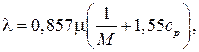
где 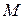– молекулярный вес данного сорта газа.

Параметры состояния газа

Вспомним объединенный газовый закон 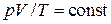(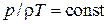), или уравнение Менделеева–Клапейрона – уравнение состояния идеального газа:

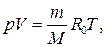или .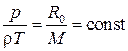

Важнейшими характеристиками состояния газа являются давление 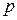, плотность 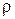и температура .

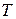В общем случае при движении газа эти параметры меняются при переходе от точки к точке и зависят от времени. Для термодинамически совершенного газа 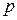, , 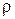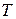связаны указанным уравнением Клапейрона. Во многих реальных практических случаях эта связь выражается более сложно. Для реальных газов нельзя пренебрегать собственным объемом молекул и силами взаимодействия между ними. Эти факторы сказываются тем сильнее, чем выше давление.

Таким образом, для неустановившегося движения параметры состояния газа являются функциями координат и времени:

, ,

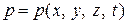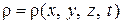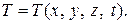
Давление. Если скорость движения жидкости V = 0, то касательные напряжения отсутствуют и в жидкости имеются только напряжения сжатия – аэродинамическое давление.

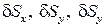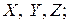
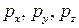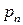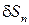Выделим в жидкости бесконечно малый тетраэдр (рис. 1.4), в котором есть плоскости граней тетраэдра, перпендикулярных к осям – давление на этих гранях; и – давление и плоскость наклонной грани, взятой произвольно.

Силы, действующие на рассматриваемый объем жидкости, разделяются на поверхностные – силы давления на грани 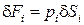и объемные – массовая сила .

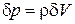Так как объем тетраэдра 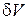есть величина третьего порядка малости, а 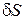– второго порядка, то при стягивании тетраэдра в точку массовой силой можно пренебречь.

Уравнение равновесия тетраэдра в проекции на ось ОX запишется как 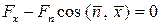, или 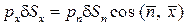. Поскольку 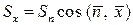, то 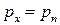. Аналогичные результаты получаются для проекций на оси OY и OZ.

Следовательно, так как координатные плоскости выбраны произвольно, то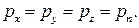

Давление в любой точке покоящейся жидкости остается постоянным для всех площадок, проходящих через эту точку, т. е. не зависит от ориентации площадки, на которую оно действует.

Единицы измерения давления следующие: в системе СИ 1 Па = 1 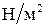; в технической системе 1 ат = 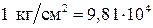Па.

Плотность. Массовая плотность характеризует распределение массы в среде. Для среды, сплошь заполняющей пространство, плотность есть функция координат точки. Массовая плотность жидкости или газа определяется как .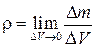

Для прерывистой среды этот предел мог бы и не существовать. При величине 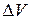, сравнимой с молекулярными размерами, непрерывное изменение 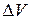привело бы к прерывистому изменению 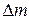. Приняв гипотезу сплошности среды, можно быть уверенным, что предел существует всегда.

Единица измерения плотности – 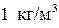. Например, при нормальных условиях (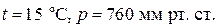) плотность воды равна 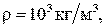а плотность воздуха 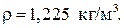Для газов плотность является функцией давления и температуры, 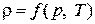, а для несжимаемых жидкостей – только температуры, .

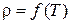Непосредственное измерение плотности движущейся сжимаемой среды затруднено, поэтому 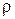обычно определяют косвенным путем. Так для совершенных газов плотность определяют с помощью уравнения Менделеева–Клапейрона, для изотермических процессов (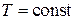) – по уравнению 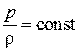, для адиабатических процессов – по уравнению 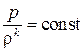, где 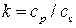– показатель адиабаты, величина которого зависит от молекулярного строения данного сорта газа; для двухатомных газов k = 1,4.

Температура. Температура есть мера внутренней энергии жидкости или газа и вообще любого тела. По величине температуры судят о степени нагретости, т. е. о тепловом состоянии тела. При наличии теплопроводности температура различных частей тела от точки к точке меняется непрерывно. Непрерывность изменения температуры возможна только в сплошных средах. Если же элементарный объем сравним с молекулярными размерами, то 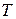– прерывистая функция (в межмолекулярном объеме температура равна нулю). Поскольку скорость хаотического движения молекул зависит от температуры, то 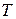является мерой кинетической составляющей внутренней энергии.

Если 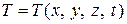, то мы имеем дело с неустановившимся (нестационарным) полем температур, если 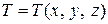, то поле температур стационарное (установившееся).

В настоящее время на равных правах существуют и применяются температурные шкалы Цельсия и Кельвина. Единица измерения температуры по шкале Цельсия – градус 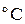, по шкале Кельвина – К (Кельвин). Переход от шкалы Цельсия к шкале Кельвина осуществляется следующим образом: 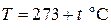(К).