Парамагнетизм

В основе классической теории парамагнетизма, созданной Ланжевеном[8] в 1905г., лежит представление, что атомы парамагнетиков обладают постоянным магнитным моментом, но взаимодействие между атомами пренебрежимо мало. В отсутствие внешнего магнитного поля магнитные моменты ориентируются случайным образом и результирующая намагниченность равна нулю. Во внешнем магнитном поле диполи будут стремиться расположиться вдоль поля, и система приобретает результирующую намагниченность, величину которой можно вычислить, пользуясь распределением Больцмана . Энергия 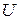определяется величиной и ориентацией магнитного момента 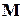во внешнем поле

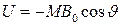, (5.44)

где 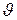– угол между направлением магнитного момента и внешнего поля (см. рис.5.15). В этом случае функция распределения 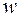приобретает вид

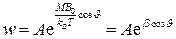, (5.45)

где .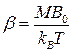

Результирующий магнитный момент определяется усреднением по всем возможным состояниям проекции момента на направление внешнего магнитного поля

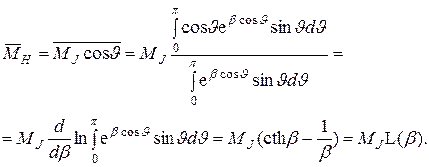(5.46)

Здесь 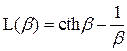есть функция Ланжевена.

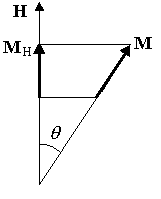Рис. 5.15. К расчету парамагнитной восприимчивости

Умножая (5.46) на концентрацию атомов 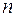(магнитных моментов), получаем намагниченность парамагнетика

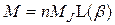. (5.47)

Для слабых полей и не слишком низких температур выполняется условие 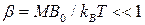. Тогда функция Ланжевена 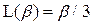и для намагниченности и восприимчивости 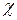парамагнетика получаем соответственно выражения

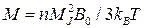; (5.48)

. (5.49)

Соотношение (5.49) называется законом Кюри-Вейсса [9]. Величина 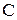является постоянной Кюри.

Введение в классическую теорию Ланжевена принципа пространственного квантования (магнитные моменты атомов во внешнем поле могут ориентироваться только под вполне определенными углами) не изменяет окончательного результата. Только в качестве 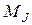необходимо использовать выражение (5.35).