Функцией распределения называют функцию 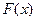 определяющую вероятность того, что случайная величина
определяющую вероятность того, что случайная величина 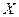 в результате испытания примет значение, меньшее
в результате испытания примет значение, меньшее 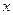 , т. е.
, т. е. 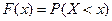 .
.
Пример 38. Дан ряд распределения случайной величины 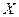 :
:
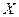 | –2 | |||
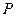 | 0,4 | 0,1 | 0,2 | 0,3 |
Составить функцию распределения 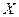 и построить ее график.
и построить ее график.
Решение:
при 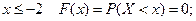
при 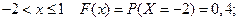
при 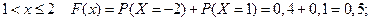
при 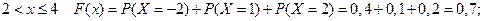
при 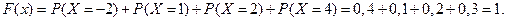
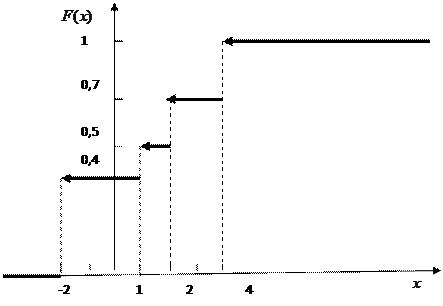 |
Рис. 1. График функции распределения
Вероятность того, что случайная величина примет значение, заключенное в интервале 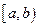 , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале: 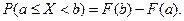
Для непрерывной случайной величины:
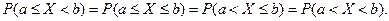 (3.9)
(3.9)
Пример 39. Случайная величина 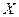 задана функцией распределения
задана функцией распределения
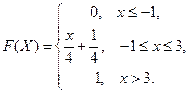
Найдите вероятность того, что в результате испытания 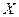 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 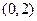 .
.
Решение. 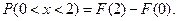 Так как на интервале
Так как на интервале 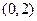
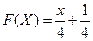 , то
, то 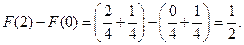 Следовательно,
Следовательно, 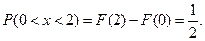
Плотностью распределения вероятностей непрерывной случайной величины 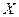 называют функцию
называют функцию 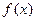 – первую производную от функции распределения
– первую производную от функции распределения 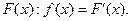
Пример 40. Дана функция распределения случайной величины  :
:
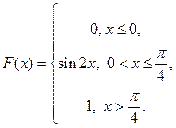
Найдите плотность распределения  .
.
Решение. Плотность распределения равна первой производной от функции распределения:
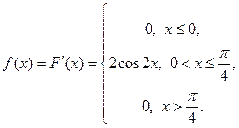
Вероятность того, что непрерывная случайная величина 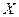 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу  равна определенному интегралу от плотности распределения, взятому в пределах от
равна определенному интегралу от плотности распределения, взятому в пределах от  до
до 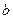 :
: 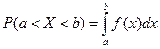 .
.
Пример 41. Задана плотность вероятности случайной величины 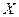
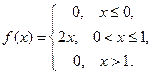
Найдите вероятность того, что в результате испытания X примет значение, принадлежащее интервалу 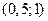 .
.
Решение. Искомая вероятность равна:
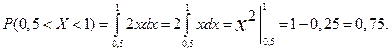
Зная плотность 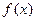 распределения можно найти функцию распределения по формуле
распределения можно найти функцию распределения по формуле 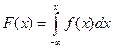 .
.
Пример 42. Найдите функцию распределения 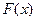 по данной плотности распределения:
по данной плотности распределения:
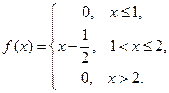
Решение. Используем формулу 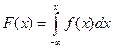 .
.
Если 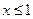 , то
, то 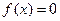 . Следовательно,
. Следовательно, 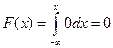 .
.
Если 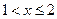 , то
, то 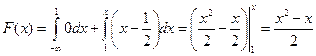 .
.
Если 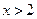 , то
, то 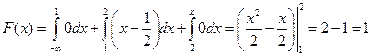 .
.
Итак, искомая функция распределения имеет вид:
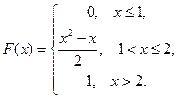
Несобственный интеграл от плотности распределения в пределах
от 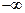 до
до 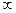 равен единице:
равен единице: 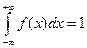 (основное условие нормировки).
(основное условие нормировки).
Пример 43. Случайная величина задана плотностью распределения
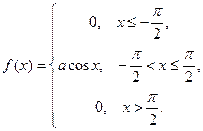
Найдите коэффициент 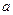 .
.
Решение. Воспользуемся формулой 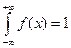 .
.
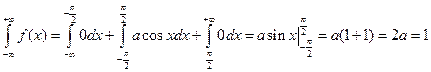 .
.
Следовательно, 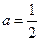 .
.
 2015-05-13
2015-05-13 45567
45567
