Несжимаемая среда. Для тонких профилей в несжимаемой жидкости, практически независимо от формы профиля
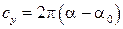 ,
, 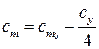 , (8.13)
, (8.13)
где 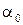 – угол атаки нулевой подъемной силы (при расчетах подставляется в формулу со своим знаком);
– угол атаки нулевой подъемной силы (при расчетах подставляется в формулу со своим знаком); 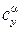 – производная, не зависящая от формы профиля и равная
– производная, не зависящая от формы профиля и равная 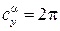 . Для симметричных профилей
. Для симметричных профилей 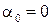 и
и 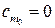 . При увеличении вогнутости профиля
. При увеличении вогнутости профиля 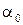 и
и 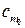 увеличиваются. Относительная толщина профиля
увеличиваются. Относительная толщина профиля 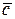 на величины
на величины 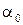 и
и 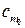 практически не влияет. При малых углах атаки
практически не влияет. При малых углах атаки 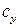 и
и 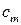 изменяются линейно.
изменяются линейно.
Характер течения в пограничном слое влияет на характеристики профиля (рис. 8.22). При переходе к турбулентному режиму течения (увеличение числа 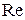 ) величина
) величина 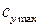 профиля возрастает (рис. 8.22, а). Это связано с тем, что турбулентный пограничный слой более устойчив к отрыву, чем ламинарный. Смещение поляры профиля к началу координат (рис. 8.22, б) связано с отмеченным выше уменьшением коэффициента сопротивления трения при увеличении числа Рейнольдса.
профиля возрастает (рис. 8.22, а). Это связано с тем, что турбулентный пограничный слой более устойчив к отрыву, чем ламинарный. Смещение поляры профиля к началу координат (рис. 8.22, б) связано с отмеченным выше уменьшением коэффициента сопротивления трения при увеличении числа Рейнольдса.
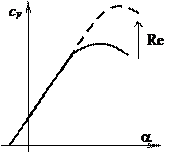

а б
Рис. 8.22. Влияние числа Рейнольдса на характеристики профиля:
а – переход к турбулентному режиму течения; б – смещение поляры профиля
к началу координат
Число 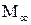 существенно влияет на величину
существенно влияет на величину 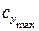 профиля. С ростом
профиля. С ростом 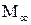
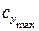 уменьшается, причем чем резче уменьшается
уменьшается, причем чем резче уменьшается 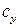 при углах атаки больших
при углах атаки больших 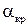 , тем сильнее снижается
, тем сильнее снижается 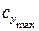 при увеличении
при увеличении 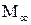 .
.
Докритические скорости. В диапазоне чисел Маха 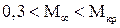 необходимо учитывать сжимаемость среды, например, через поправку Прандтля–Глауэрта:
необходимо учитывать сжимаемость среды, например, через поправку Прандтля–Глауэрта: 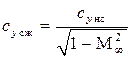 .
.
Закритические скорости. При 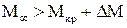 вначале
вначале 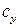 растет вследствие увеличения разрежения на верхней части профиля. Рост протяженности местной сверхзвуковой зоны приводит к тому, что в результате взаимодействия скачка уплотнения с турбулентным пограничным слоем происходит отрыв потока в области диффузорного течения (в кормовой части профиля). Развитие течения на верхней поверхности из-за отрыва замедляется (рис. 8.23), и замедляется рост
растет вследствие увеличения разрежения на верхней части профиля. Рост протяженности местной сверхзвуковой зоны приводит к тому, что в результате взаимодействия скачка уплотнения с турбулентным пограничным слоем происходит отрыв потока в области диффузорного течения (в кормовой части профиля). Развитие течения на верхней поверхности из-за отрыва замедляется (рис. 8.23), и замедляется рост 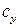 . Затем аналогичное развитие течения происходит на нижней поверхности, где также образуется сверхзвуковое течение, которое в своем развитии догоняет и обгоняет верхнюю сверхзвуковую зону. Вследствие этого в задней части профиля появляется отрицательная подъемная сила (рис. 8.23,
. Затем аналогичное развитие течения происходит на нижней поверхности, где также образуется сверхзвуковое течение, которое в своем развитии догоняет и обгоняет верхнюю сверхзвуковую зону. Вследствие этого в задней части профиля появляется отрицательная подъемная сила (рис. 8.23, 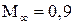 ), приводящая к уменьшению подъемной силы и момента тангажа профиля. Причем коэффициент момента для некоторых профилей может резко сменить знак, что приводит к нарушению балансировки ЛА.
), приводящая к уменьшению подъемной силы и момента тангажа профиля. Причем коэффициент момента для некоторых профилей может резко сменить знак, что приводит к нарушению балансировки ЛА.

Рис. 8.23. Зависимости:
а – 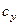 и
и 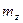 профиля от числа Маха; б – распределения коэффициента давления
профиля от числа Маха; б – распределения коэффициента давления
(–––– – верхняя часть профиля; - - - - – нижняя часть профиля)
и схемы течения для некоторых чисел Маха
Сверхзвуковые скорости. При 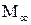 > 1 для приближенного расчета коэффициента подъемной силы симметричного профиля можно использовать формулу
> 1 для приближенного расчета коэффициента подъемной силы симметричного профиля можно использовать формулу 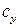 =
= 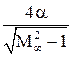 , полученную по линейной теории для плоской пластинки. Тогда для несимметричного профиля
, полученную по линейной теории для плоской пластинки. Тогда для несимметричного профиля 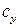 =
= 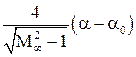 .
.
 2015-03-22
2015-03-22 1298
1298








