1. Имеется сферический (цилиндрический) конденсатор (рис.1.12)
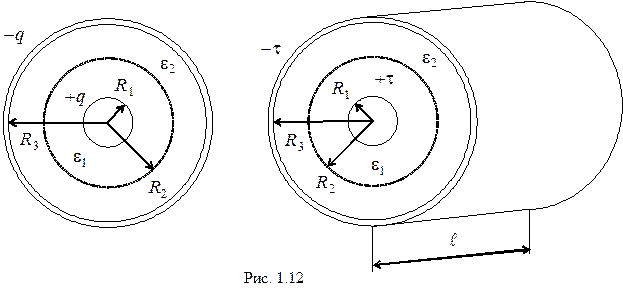
с двумя слоями диэлектрика. Радиусы обкладок 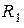 и
и 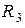 , радиус границы раздела диэлектриков с диэлектрическими проницаемостями
, радиус границы раздела диэлектриков с диэлектрическими проницаемостями 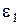 и
и 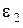 равен
равен 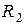 . Заряд сферического конденсатора
. Заряд сферического конденсатора 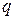 (для цилиндрического конденсатора задается линейная плотность заряда
(для цилиндрического конденсатора задается линейная плотность заряда 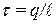 ). Определить зависимости
). Определить зависимости 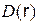 ,
, 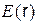 ,
, 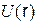 и изобразить их в виде графиков. Вывести выражение для емкости конденсатора.
и изобразить их в виде графиков. Вывести выражение для емкости конденсатора.
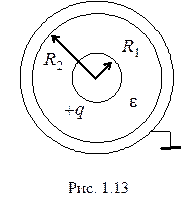 2. Заряженный проводящий шар радиусом
2. Заряженный проводящий шар радиусом 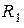 (рис.1.13) окружен слоем диэлектрика с диэлектрической проницаемостью
(рис.1.13) окружен слоем диэлектрика с диэлектрической проницаемостью 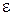 и проводящим сферическим экраном. Внутренний радиус экрана
и проводящим сферическим экраном. Внутренний радиус экрана 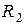 . Экран заземлен. Построить графики зависимостей
. Экран заземлен. Построить графики зависимостей 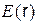 ,
, 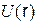 .
.

3. Построить графики изменения напряженности электрического поля 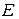 , потенциала
, потенциала 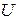 в функции от расстояния
в функции от расстояния 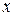 в плоском конденсаторе с двумя слоями диэлектрика (рис.1.14). Получить выражение для емкости конденсатора, если площадь его пластин
в плоском конденсаторе с двумя слоями диэлектрика (рис.1.14). Получить выражение для емкости конденсатора, если площадь его пластин 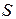 . Для каждого слоя диэлектрика известны абсолютная диэлектрическая проницаемость (
. Для каждого слоя диэлектрика известны абсолютная диэлектрическая проницаемость (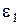 ,
, 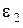 ) и толщина (
) и толщина (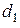 ,
, 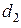 ). Искривлением силовых линий у краев пластин конденсатора пренебречь.
). Искривлением силовых линий у краев пластин конденсатора пренебречь.

4. Абсолютная диэлектрическая проницаемость изоляции коаксиального кабеля изменяется обратно пропорционально расстоянию 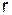 от оси кабеля
от оси кабеля 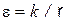 . Радиус жилы кабеля
. Радиус жилы кабеля 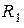 , внутренний радиус оболочки
, внутренний радиус оболочки 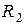 , напряжение между жилой и оболочкой
, напряжение между жилой и оболочкой 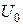 . Получить зависимости
. Получить зависимости 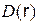 ,
, 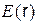 ,
, 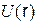 и построить их в виде графиков, рассматривая отрезок кабеля длиной
и построить их в виде графиков, рассматривая отрезок кабеля длиной 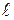 .
.
 2015-03-22
2015-03-22 503
503








