2015-03-22
676
При расчете электрических цепей используются законы Кирхгофа. Первый закон Кирхгофа формулируется применительно к узлам электрической цепи и следует из принципа непрерывности электрического тока: алгебраическая сумма токов всех ветвей, имеющих общий узел, равна нулю
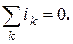
Принято знак “плюс” приписывать току ветви, условное положительное направление которого направлено от узла, “минус” - к узлу. Например:
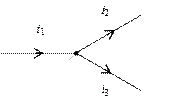
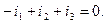
Второй закон Кирхгофа формулируется применительно к контурам электрической цепи: алгебраическая сумма падений напряжений во всех ветвях любого контура электрической цепи равна алгебраической сумме э.д.с., действующих в этом контуре
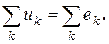
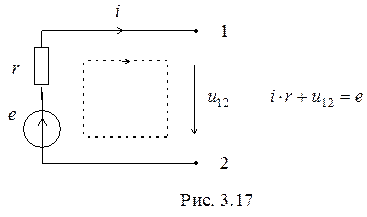При использовании второго закона Кирхгофа задаются произвольным положительным направлением обхода контура. Напряжения и э.д.с., условные положительные направления которых совпадают с направлением обхода, берутся со знаком “плюс”, в противном случае напряжения и э.д.с берутся со знаком “минус”.
Особо отметим, что при составлении уравнения по второму закону Кирхгофа контур может проходить не только по ветвям графа схемы, но и иметь вид, подобный указанному пунктиром на рис.3.17.
По первому закону Кирхгофа можно составить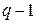 
линейно независимых уравнений для 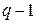узла.
По второму закону Кирхгофа число линейно независимых уравнений равно числу связей графа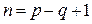 
. Действительно, любая связь графа образует контур с ветвями дерева и каждый такой контур отличается от остальных контуров по крайней мере ветвью, образующей связь. Таким образом, число независимых контуров .
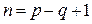Общее число уравнений, составленных по первому и второму законам Кирхгофа, равно числу ветвей графа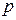 
. Если неизвестными электрической схемы являются напряжения 
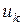и токи 
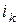в 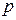ветвях, то для записи полной системы уравнений необходимо добавить уравнения, связывающие напряжения 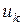и токи 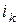на элементах электрической цепи (число таких уравнений равно числу пассивных элементов схемы электрической цепи).
Выражая напряжения на элементах 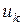через токи 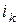в уравнениях, составленных по второму закону Кирхгофа, получим систему 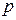уравнений относительно 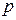неизвестных токов 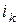в ветвях.
При расчете электрической цепи с зависимыми источниками уравнения формируются в два этапа:
· составляются уравнения цепи в предположении, что все источники независимые;
· слагаемые уравнений, соответствующие зависимым источникам, выражаются через управляющие токи и напряжения.
Пример. Составить уравнения по законам Кирхгофа для определения токов в ветвях электрической схемы (рис.3.16), считая известными параметры элементов схемы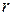 
, 
, 
, 
, 
.
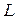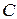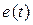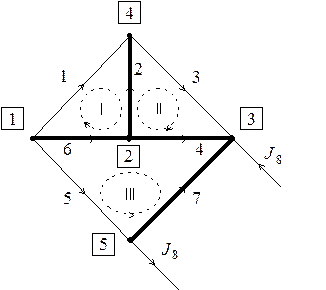Граф этой схемы имеет вид
Число узлов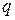 
= 5, число ветвей
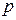= 7.
Число уравнений по первому закону Кирхгофа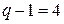 
. Для узлов с первого по четвертый имеем:
1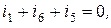 
2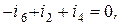 
3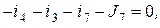 
4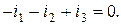 
Число независимых контуров 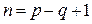= 3 равно числу связей. Выберем независимые контуры, каждый из которых образован одной связью (тонкие линии на рисунке графа) и ветвями дерева (утолщенные линии). Направления обхода контуров примем совпадающими с условными положительными направлениями токов в связях. Выражая напряжения на отдельных элементах цепи через токи ветвей, получим три уравнения, составленные по второму закону Кирхгофа:
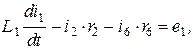
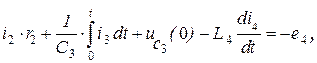
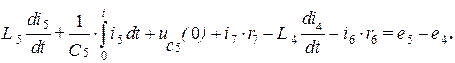
Решая полученную систему из семи уравнений, можно определить токи во всех ветвях схемы.
