Метод симметричных составляющих

Любая несимметричная трехфазная система э.д.с., напряжений, токов может быть представлена в виде суммы трех симметричных систем - нулевой, прямой и обратной последовательностей, называемых симметричными составляющими несимметричной трехфазной системы.

Рассмотрим, например, несимметричную трехфазную систему э.д.с. 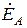, , 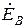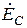. Представим эти э.д.с. в виде суммы трех слагаемых таким образом, чтобы первые из них образовывали в трех фазах симметричную систему нулевой последовательности 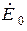, , 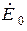, 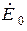вторые - симметричную систему прямой последовательности 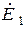, , 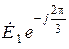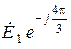и третьи - симметричную систему обратной последовательности 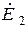, , 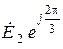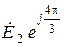Для удобства дальнейшего анализа введем обозначение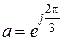

Отметим некоторые свойства оператора :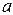

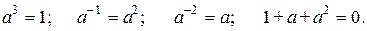
Запишем теперь выражения для э.д.с. в отдельных фазах:

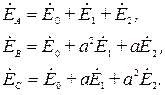
Доказательством возможности такого представления является то, что система трех уравнений с тремя неизвестными и с неравным нулю определителем всегда имеет единственное решение:

(*)

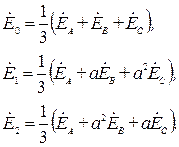Полученные соотношения иллюстрирует рисунок, на котором осуществлено графическое построение векторов 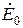, , 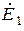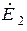по произвольно ориентированным друг относительно друга векторам 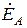, , 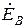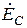. С этой целью проведено графическое преобразование векторов 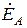, , 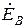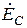в соответствии с соотношениями (*). При построении использовался тот факт, что умножение вектора на множитель а эквивалентно его повороту на 120 градусов против часовой стрелки.

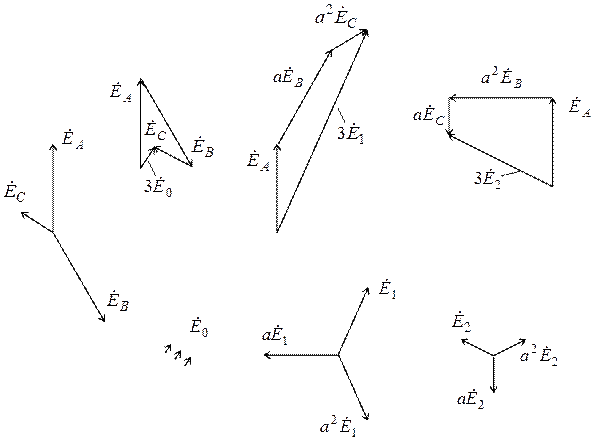
На основе полученных графически векторов , , 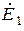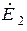построены симметричные системы нулевой, прямой и обратной последовательностей.

Рассмотренное разложение может быть использовано для расчета несимметричного режима трехфазной цепи. Подобный подход к решению задачи становится особенно ценным, когда сопротивление цепи имеет различные значения для различных симметричных составляющих. Такая ситуация возникает, например, при анализе электрических цепей, содержащих электрические машины.

В качестве примера применения метода симметричных составляющих рассмотрим случай однофазного короткого замыкания на землю в трехфазном источнике э.д.с. прямой последовательности (трехфазном генераторе).

На рисунке 11.7 фазы " В " и " С " обесточены, поскольку токами нормальной нагрузки по сравнению с током короткого замыкания можно пренебречь. Нейтральная точка генератора заземлена через сопротивление 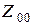, включающее в себя и сопротивление растекания тока в земле.

Разложим системы токов, напряжений и э.д.с. на симметричные составляющие и запишем связывающие их уравнения:

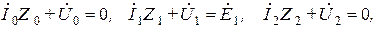
где 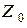, , 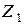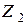- эквивалентные сопротивления цепи для нулевой, прямой и обратной последовательностей.

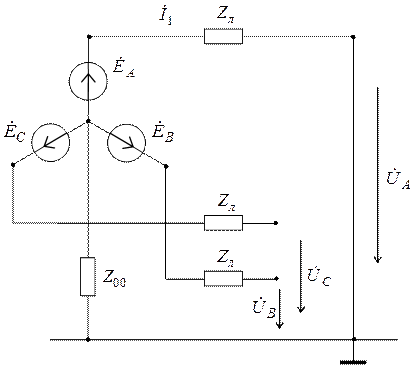
Правые части первого и третьего уравнений равны нулю, так как источник э.д.с. представляет собой трехфазную систему прямой последовательности ().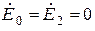

При сложении записанных уравнений получим

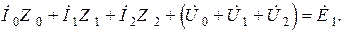
Примем во внимание, что 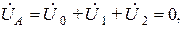тогда

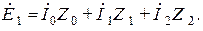
Поскольку, как видно из приведенной схемы, 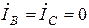, для симметричных составляющих системы токов имеем

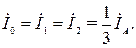
Учитывая эти соотношения, получаем:

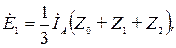
откуда

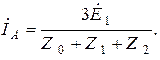
Запишем выражения для симметричных составляющих напряжения в месте короткого замыкания:

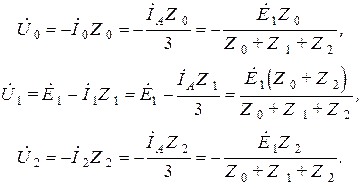
Напряжения фаз " В " и " С " определяться в виде:

Приведенные выражения для симметричных составляющих напряжений получены в предположении, что сопротивления цепи для токов прямой и обратной последовательностей различны. Если же считать эти сопротивления одинаковыми, то, воспользовавшись результатами решения рассмотренных ранее задач для симметричных режимов, запишем:

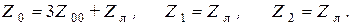
С учетом этих соотношений выражения для симметричных составляющих напряжения и фазного тока примут вид

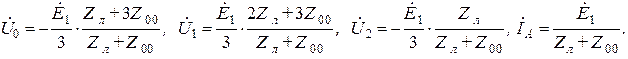Последнее соотношение может быть получено из уравнения, составленного на основе второго закона Кирхгофа для контура, включающего в себя фазу " А " и нулевой провод

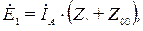
однако, как уже отмечалось, такой простой способ решения может быть применен только при равенстве сопротивлений для токов прямой и обратной последовательностей.