Метод итераций позволяет получить последовательность приближенных значений, сходящуюся к точному решению системы линейных уравнений. В отличие от метода Гаусса, метод итераций не требует контроля промежуточных вычислений, так как отдельные ошибки на каком-либо шаге итерации не искажают окончательных результатов, хотя и удлиняет процесс счета. Иначе говоря, метод итераций решения систем линейных уравнений является самоисправляющимся. Кроме того, метод итераций легко запрограммировать для ЭВМ. Пусть имеем систему
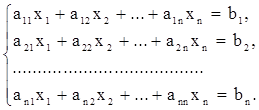 или, короче,
или, короче, 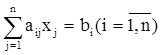 .
.
Предположим, что определитель системы отличен от нуля и что диагональные коэффициенты 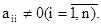 Выразим из первого уравнения x1, из второго x2, и т. д. Тогда получим эквивалентную систему:
Выразим из первого уравнения x1, из второго x2, и т. д. Тогда получим эквивалентную систему:
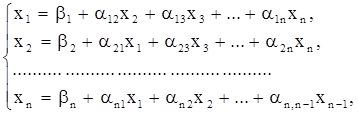 ,
,
где 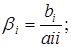

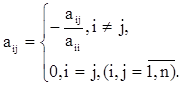
Полученную систему запишем так:
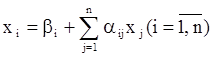 (3)
(3)
и назовем ее системой нормального вида.
Будем решать ее методом последовательных приближений. За нулевое приближение возьмем, например, столбец свободных членов
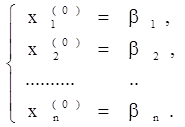
Подставив в правую часть системы (3) значения 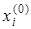 (i =
(i = 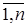 ), получим первое приближение:
), получим первое приближение:
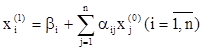 .
.
Затем аналогично второе: 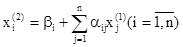 и т. д.
и т. д.
Таким образом, зная k- e приближение, (k + 1)-е приближение вычисляют по формуле
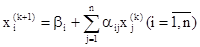 (4)
(4)
Если последовательность приближений (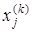 ) (j =
) (j = 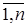 ) имеет предел
) имеет предел 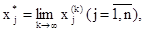 то
то 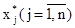 является точным решением системы нормального вида, а значит, и исходной системы. В самом деле, переходя к пределу при
является точным решением системы нормального вида, а значит, и исходной системы. В самом деле, переходя к пределу при 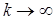 в (4), имеем:
в (4), имеем:
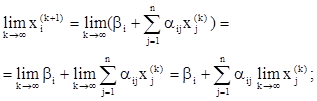
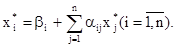
Описанный метод последовательных приближений называется методом итераций. Рабочие формулы метода итераций имеют вид:
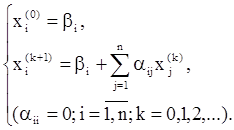
Существование предела 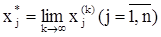 гарантирует теорема о достаточном признаке сходимости процесса итераций.
гарантирует теорема о достаточном признаке сходимости процесса итераций.
Достаточным условием сходимости итерационных методов является условие
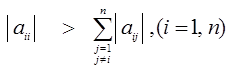
При методе Зейделя итерационный процесс подобен описанному для метода простых итераций, однако уточненные значения Хij+1 сразу подставляются в последующие уравнения. Формула итерационного процесса имеет вид:
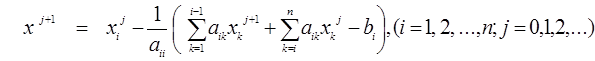
 2015-03-22
2015-03-22 676
676








