Если цена приобретения купонной облигации соответствует ее номинальной стоимости, то доходность по такой облигации равна ее купонной доходности.
Часто бывает, что рыночная цена купонной облигации отличается от ее номинальной стоимости. Такая ситуация может возникнуть, например, если после того, как облигация была выпущена, уровень процентных ставок в экономике начал понижаться. Допустим, что наша 10%-ная купонная облигация была выпущена 19 лет тому назад как облигация со сроком погашения через 20 лет. В то время на кривой доходности облигации аналогичного инвестиционного качества и со сроком погашения 1 год рз полагались на уровне доходности 10% в год. Сейчас до окончания срока погашения остался один год, но теперь процентная ставка по аналогичным годовым облигациям составляет 5%.
Хотя 10%-ная купонная облигация была выпущена по номиналу (1000 долл.), ее сегодняшняя рыночная цена составляет 1047,62. В связи с тем, что цена облигации теперь превышает ее номинальную стоимость, она называется облигацией с премией (премиальной облигацией) (premium bond).
Какова доходность такой облигации?
Существует два различных показателя доходности, которые можно рассчитать. Первый — это текущая доходность (current yield), которая рассчитывается путем деления суммы платежа по годовому купону на рыночную цену облигации:
Текущая доходность= Купон / Цена = 100/1047,62 = 9,55%
Текущая доходность превышает действительную доходность премиальной облигации. Это связано с тем, что не учитывается тот факт, что на момент погашения будет выплачено только 1000 долл., т.е. на 47,62 долл. меньше, чем было заплачено за облигацию.
Для того чтобы принять во внимание тот факт, что номинальная стоимость облигации может отличаться от ее рыночной цены, рассчитаем доходность, называемую доходностью при погашении (yield-to-maturity). Доходность при погашении (ее еще называют доходностью к погашению и полной доходностью) можно рассматривать как дисконтную ставку, при которой приведенная стоимость ожидаемых денежных платежей по облигации равнялась бы ее текущей цене.
Доходность при погашении учитывает все денежные платежи, которые получит владелец облигации, включая номинальную стоимость облигации на момент ее погашения (1000 долл.). В данном случае, в связи с тем, что срок погашения облигации наступает через один год, расчет доходности при погашении не представляет особой сложности:
Доходность при погашении = (Купон + Номинал - Текущая цена) / Текущая цена
Доходность при погашении
= (100 долл. + 1000 долл. – 1047,62 долл.) / 1047,62 долл. = 5%
Таким образом, если бы при расчете ставки доходности, на которую рассчитывает покупатель облигации, использовался показатель текущий доходности (9,55%), то это привело бы к серьезным заблуждениям.
Если срок погашения облигации превышает один год, то расчет ее доходности при погашении намного более сложен, чем в предыдущем примере. Предположим, что вы Рассматриваете возможность покупки двухгодичной 10%-ной купонной облигации, имеющую номинальную стоимость 1000 долл. и текущую цену 1100 долл. Какова ее Доходность?
Ее текущая доходность равняется 9,09%.
Текущая доходность = Купон / Цена = 100 долл. / 1000 долл. = 9,09%
Однако, так же как и в случае с годичной премиальной облигацией, показатель текущей доходности не учитывает того, что на момент погашения вы получите меньше, чем платили (1100 долл.). В ситуации, когда время до погашения облигации превышает один год, доходность при погашении представляет собой ставку дисконтирования, при которой приведенная стоимость ожидаемых денежных поступлений равнялась бы текущей цене облигации.
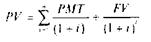
где n - количество ежегодных платежных периодов до момента погашения облигации, i — годовая доходность при погашении, РМТ' — купонный платеж, FV— номинальная стоимость облигации.
Доходность при погашении по купонной облигации с периодом погашения свыше одного года может быть вычислена с помощью специализированного калькулятора с финансовыми функциями, в который необходимо ввести следующие значения: п — количество ежегодных платежных периодов до момента погашения облигации, PV— цена облигации (со знаком "минус"), FV— ее номинальная стоимость, РМТ -— купонный платеж по облигации.
| n | i | PV | FV | РМГ | Результат |
| -1100 | i= 4,65% |
Таким образом, доходность при погашении по этой двухгодичной премиальной облигации значительно меньше текущей доходности.
Данный пример иллюстрирует основное правило, описывающее отношение между ценами облигаций и их доходностью.
 2015-03-07
2015-03-07 527
527








