Статические режимы СУ ЭП характеризуются установившимися состояниями при неизменных входных воздействиях. Уравнения статики легко получить из уравнений динамики СУ ЭП, приравняв в них нулю все производные по времени переменных (координат состояния) и внешних воздействий. В операторных уравнениях и структурных схемах линейных САУ это эквивалентно приравниванию нулю оператора p. Таким образом, статическая характеристика системы – это зависимость выходной переменной от какой-либо входной переменной в статическом (установившемся) режиме.
Примером статической характеристики является механическая характеристика электропривода – зависимость угловой частоты вращения вала двигателя от момента нагрузки на валу в установившихся режимах. Для электропривода постоянного тока такая характеристика приведена на рис. 5.1.
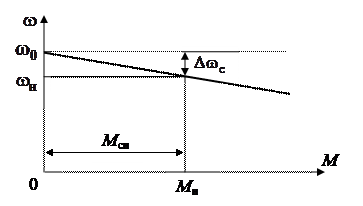 |
Рис. 5.1. Статическая механическая характеристика
двигателя постоянного тока
Как видим, при увеличении нагрузки на валу двигателя скорость вращения вала двигателя падает и появляется статическая ошибка регулирования скорости. При изменении нагрузки от нуля до номинального значения M сн скорость вращения уменьшается от скорости холостого хода 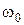 до номинальной скорости
до номинальной скорости 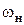 . В номинальном режиме абсолютная величина статической ошибки регулирования скорости вращения
. В номинальном режиме абсолютная величина статической ошибки регулирования скорости вращения
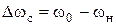 . (5.1)
. (5.1)
Найдем выражения для установившейся ошибки регулирования в общем случае изменения задающих или возмущающих воздействий линейной СУ ЭП.
Передаточная функция любого замкнутого контура регулирования электропривода с отрицательной обратной связью (рис. 5.2) определяется передаточными функциями прямого 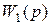 и обратного
и обратного 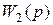 каналов регулирования [3]:
каналов регулирования [3]:
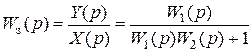 . (5.2)
. (5.2)
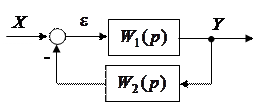 |
Рис. 5.2. Структурная схема замкнутого контура регулирования
Отсюда изображение ошибки регулирования в системе
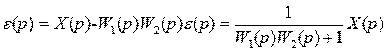 , (5.3)
, (5.3)
а передаточная функция по ошибке
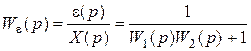 . (5.4)
. (5.4)
Как следует из (54.3), ошибка регулирования будет стремиться к нулю при X = const, если 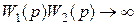 , что предполагает реализацию бесконечно большого усиления в устройстве управления и может привести к неустойчивости системы. Кроме того, реальные динамические звенья обладают конечными коэффициентами усиления, что приводит к возникновению ненулевой статической ошибки регулирования.
, что предполагает реализацию бесконечно большого усиления в устройстве управления и может привести к неустойчивости системы. Кроме того, реальные динамические звенья обладают конечными коэффициентами усиления, что приводит к возникновению ненулевой статической ошибки регулирования.
Между тем, статическая ошибка регулирования в системе при неизменном входном воздействии может быть сведена к нулю, если сделать равной нулю передаточную функцию ошибки 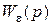 по задающему (возмущающему) воздействию при p =0. Для этого достаточно в прямой или обратный канал регулирования системы, приведенной два рис. 5.2, ввести интегрирующее звено. На практике интегрирующее звено вводят в структуру устройства управления, применяя И-, ПИ-, ПИД-регуляторы. Это обеспечивает
по задающему (возмущающему) воздействию при p =0. Для этого достаточно в прямой или обратный канал регулирования системы, приведенной два рис. 5.2, ввести интегрирующее звено. На практике интегрирующее звено вводят в структуру устройства управления, применяя И-, ПИ-, ПИД-регуляторы. Это обеспечивает 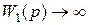 и, тем самым, нулевую статическую ошибку регулирования. Такие системы принято называть астатическими нулевого порядка по задающему или (и) возмущаещему воздействию. Для придания системе астатизма более высокого порядка в структуру регулятора вводят соответствующее число интеграторов.
и, тем самым, нулевую статическую ошибку регулирования. Такие системы принято называть астатическими нулевого порядка по задающему или (и) возмущаещему воздействию. Для придания системе астатизма более высокого порядка в структуру регулятора вводят соответствующее число интеграторов.
Величина установившейся ошибки регулирования, наличие и порядок астатизма замкнутой САУ определяются не только ее моделью, но и видом входного сигнала. Определим, как вид входного воздействия влияет на величину установившейся ошибки.
Передаточную функцию прямого канала СУ ЭП запишем в виде
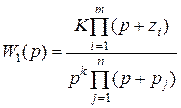 , (5.5)
, (5.5)
где K – коэффициент передачи,
pj, zi – полюсы и нули передаточной функции (5.5).
Для определения величины установившейся ошибки рассмотрим случай единичной обратной связи, т. е. 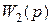 =1.
=1.
В установившихся режимах (при p = 0) передаточную функцию (5.4) можно записать в виде
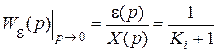 , (5.6)
, (5.6)
где Ki – коэффициент ошибки системы, определяемый видом входного воздействия, i = 0, 1, 2.
Поскольку в качестве типовых тестовых сигналов применяют ступенчатое, линейное и квадратичное входное воздействие, то для оценки установившихся ошибок в системе выделяют 3 типа коэффициентов ошибок:
1) коэффициент ошибки по положению (i = 0)
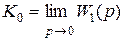 ; (5.7)
; (5.7)
2) коэффициент ошибки по скорости (i = 1)
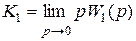 ; (5.8)
; (5.8)
3) коэффициент ошибки по ускорению (i = 2)
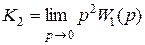 . (5.9)
. (5.9)
Как следует из выражений (5.3)…(5.9), установившиеся ошибки СУ ЭП могут иметь нулевое, бесконечное или постоянное значение в зависимости от числа интеграторов в передаточной функции W 1(p) и типа входного сигнала. Установившиеся ошибки для трех типов входных воздействий и трех типов передаточной функции W 1(p) – с отсутствием интеграторов, с одним и с двумя интеграторами – приведены в табл. 5.1.
Табл. 5.1
| Число интеграторов | Входной сигнал | ||
Ступенчатый 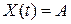 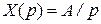 | Линейный 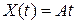 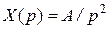 | Квадратичный 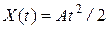 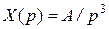 | |
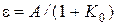 | 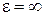 | 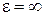 | |
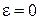 | 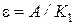 | 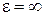 | |
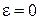 | 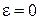 | 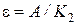 |
 2015-03-22
2015-03-22 2107
2107
