Основные понятия теории алгоритмов

В этой книге алгоритмы обсуждаются в разных главах и в двух различных аспектах. Первый аспект — теоретический, и его обсуж дению посвящен данный раздел, а второй — прагматический, тесно связанный с программированием, и излагается в седьмой главе.

Теория алгоритмов — раздел математики, изучающий общие свойства алгоритмов. Понятие «алгоритм» сформировалось в мате матике в 20-х годах XX в. Началом систематической разработки теории алгоритмов можно считать 1936 г. и связывают это начало с публикацией работы А.А. Черча.

Под алгоритмом всегда (и до возникновения строгой теории) понималась процедура, которая позволяла путем выполнения после довательности элементарных шагов получать однозначный результат (независящий от того, кто именно выполнял эти шаги) или за конечное число шагов прийти к выводу о том, что решения не существует.

Конечно же это нестрогое определение понятия алгоритма и именно попытки сформулировать такое понятие привели к возник новению теории алгоритмов. Причиной развития этой теории были внутренние проблемы математики и лишь с возникновением и развитием вычислительной техники и 'смежных наук выяснилось, что в основе этих наук должна лежать теория алгоритмов. Так стало очевидным прикладное значение новой науки.

В основе формализации понятия «алгоритм» лежит идея построения алгоритмической модели. Составляющими такой модели должны быть конкретный набор элементарных шагов, способы определения следующего шага и т.д. От модели также требуется простота и универсальность. Требование простоты важно для того,

чтобы выделить действительно необходимые элементы и свойства алгоритма и облегчить доказательства общих утверждений об этих свойствах. Универсальность необходима для того, чтобы модель позволяла описать любой алгоритм.

Результатами теоретических исследований явились три основных класса арифметических моделей.

Первый класс моделей основан на арифметизации алгоритмов. Предполагается, что любые данные можно закодировать числами, и как следствие — всякое их преобразование становится в этом случае арифметическим вычислением, алгоритмом в таких моделях есть вычисление значения некоторой числовой функции, а его элемен тарные шаги — арифметические операции. Последовательность ша гов определяется двумя способами. Первый способ — суперпозиция, т.е. подстановка функции в функцию, а второй — рекурсия, т.е. определение значения функции через «ранее» вычисленные значения этой же функции. Функции, которые можно построить из целых чисел и арифметических операций с помощью суперпозиций и рекурсивных определений, называются рекурсивными функциями. Простейшим примером рекурсивной функции является факториал:

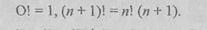
Другие примеры рекурсивной функции можно найти в разделе 7,2.

Второй класс моделей порожден следующей идеей. Для того чтобы алгоритм понимался однозначно, а его каждый шаг считался элементарным и выполнимым, он должен быть представлен так, чтобы его могла выполнять машина, к которой предъявляются уже упомянутые требования простоты и универсальности. Одной из таких машин явилась абстрактная машина Тьюринга. Машина Тьюринга

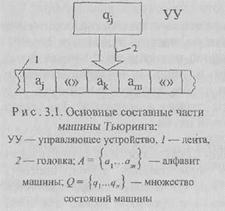состоит из трех частей (рис. 3.1): ленты, головки и управляющего устройства (УУ). Лента беско нечна в обе стороны и разбита на ячейки. В каждой ячейке может быть записан только один символ.

Отсутствие символа в ячейке обозначается специальным «пус тым» символом «». Головка всег да располагается над некоторой ячейкой ленты. Она может читать и писать символы, стирать их и

перемещаться вдоль ленты. Число возможных символов конечно, и образуют алфавит машины Л={<7_Ь...,#„,}. Головка в каждый такт работы машины находится в одном из состояний. Множество таких состояний конечно Q = {q\,...₉q_n} и среди них выделяют начальное q_l и конечное q_z состояния.

Элементарный шаг машины Тьюринга состоит из следующих действий:

головка считывает символ, записанный в ячейке, над которой она находится;

считанный символ а* и текущее состояние головки д/ однозначно определяют новое состояние #,, новый записываемый символ #i и перемещение головки d_p (которое может иметь значение на ячейку влево, на ячейку вправо, остаться на месте).

Устройство управления хранит и выполняет команды машины вида qjOt -> qfl\d_p.

Конкретную машину Тьюринга (и алгоритм соответственно) можно задать, перечислив элементы AttQn команды машины.

Полное состояние машины Тьюринга называется конфигурацией и включает в себя состояние головки, состояние ленты (слово, записанное за ней) и положение головки на ленте. Конфигурация описывается тройкой a\qa^, где q — текущее состояние головки, о\ — слово слева, а а₂ — слово справа от головки (включая символ, над которым находится головка). Конфигурация, изображенная на рис. 3.1., может быть записана так: а/«» gj a_k a_m.

Перед началом работы на пустую ленту записывается исходное слово а конечной длины, головка устанавливается над первым его символом и, как следствие, начальной конфигурацией является q\a.

Третий класс моделей алгоритмов очень близок к предыдущему,
но не оперирует конкретными машинными механизмами. Наиболее
известная алгоритмическая модель этого типа нормальные

алгоритмы Маркова.

Для нормального алгоритма задается алфавит, над которым он работает, конечное множество допустимых подстановок и порядок их применения. Если в качестве алфавита взять алфавит русского языка, а в качестве множества подстановок

то, используя правила 1—J:

1) проверить возможность подстановок в порядке возрастания их
номеров, и если она возможна (левая часть подстановки обнаружена в
исходном слове), произвести подстановку (заменив левую часть на
правую);

2) если в примененной подстановке имеется символ «!», то
преобразования прекращаются, а если нет, то текущее состояние
становится исходным и весь процесс начинается заново;

3) если ни одна подстановка не применима, то процесс преобра
зования завершен,

можно обнаружить, что по заданному алгоритму исходное слово «слон» превращается в слово «муха» по следующей цепочке:

«слон» —> «суон» —» «муон» —> «мухн» —> «муха».

В теории алгоритмов строго доказано, что по своим возмож ностям преобразования нормальные алгоритмы эквивалентны машине Тьюринга и другим моделям, уточняющим понятия алго ритма.

Появление точного понятия алгоритма позволило сформу лировать алгоритмически не разрешимые проблемы, т.е. задачи, для решения которых невозможно построить алгоритм. Задача назы вается алгоритмически неразрешимой, если не существует машины Тьюринга (или рекурсивной функции, или нормального алгоритма Маркова), которая ее решает. Например, неразрешимой оказалась проблема распознавания эквивалентности алгоритмов: нельзя постро ить алгоритм, который по любым двум алгоритмам (программам) выяснял бы, вычисляют они одну и ту же функцию или нет. Знание основных неразрешимостей теории алгоритмов необходимо для специалиста по информатике. Оно предостережет его от увлечения глобальными прожектами всеобщей алгоритмизации точно так же, как знание основных законов физики предостерегает от попыток создания вечного двигателя.