2015-03-22
402
Вычисляем потенциалы строк и столбцов матрицы поставок из уравнений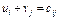 
, составленных для каждой заполненной клетки таблицы.
Затем, по известным потенциалам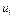 
и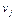 
вычисляем оценки свободных клеток: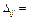 
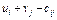
Если все оценки свободных клеток неположительны, то найденное решение оптимально.
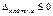
Переход к новому решению:
Если обнаружена свободная клетка таблицы поставок, не удовлетворяющая критерию оптимальности, из неё строим цикл, вычисляем величину сдвига по циклу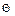 
, если 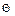>0, осуществляем сдвиг по этому циклу и получаем новое опорное решение.
