2015-03-22
446
Транспортные задачи – целочисленные задачи линейного программирования в канонической форме, коэффициенты при переменных в ограничениях равны нулю или единице и каждая переменная входит в систему ограничений два раза. Эти задачи можно решать обычным симплекс-методом, но мы рассмотрим более удобные специальные методы решения транспортных задач.
Дано: Несколько (m) поставщиков однородного товара хотят передать этот товар нескольким (n) потребителям. Мощность i го поставщика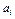 
- равна запасам товара у этого поставщика. Мощности поставщиков заносятся в первый столбец таблицы поставок. Мощность j -го потребителя - 
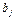- определяется количеством необходимого ему товара. Мощности потребителей равны их запросам. Известна стоимость перевозки единицы товара от каждого из поставщиков к каждому потребителю - 
.
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| ||||
| 
| 
| 
|
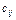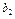
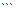
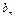
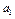
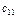
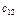
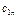
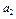
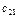
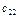
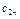
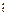
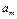
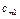
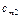
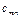
Задача: Для каждой пары «поставщик-потребитель» определить объём перевозки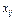 
, то есть составить оптимальныйплан перевозок товара.
|
|
|
|
|
|
|
| |
|
| 
| 
| 
| |
|
| 
| 
| 
| |
|
| ||||
|
| 
| 
| 
|
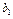
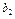
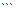
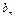
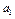
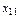
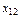
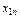
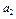
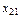
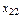
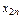
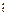
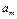
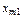
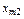
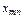
Полученная матрица перевозок должна удовлетворять следующим условиям:
1) суммарные затраты на перевозку минимальны;
 
|
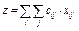
(Сумма затрат на перевозку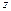 
равна сумме произведений объёмов перевозок товара 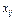на их стоимости )
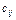2) мощности всех поставщиков реализованы; 3) запросы всех потребителей удовлетворены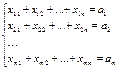 
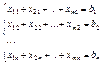
В транспортной задаче n+m уравнений ограничений, n.m переменных; из них n+m+1 линейно независимых уравнений и 
n+m+1 базисных переменных (заполненных клеток в таблице поставок). Число свободных клеток n.m – (n+m+1) равно числу свободных переменных задачи.
