I. Теория множеств – это раздел математики, изучающий абстрактные множества элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или элементами других множеств.
Задача 1. Дано: два множества А и В, множество А включает элементы 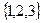 ,
,
а В – элементы 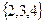 . Требуется: объединение, пересечение, разность и дизъюнктивную сумму множеств А и В.
. Требуется: объединение, пересечение, разность и дизъюнктивную сумму множеств А и В.
Решение: 1. Объединение (сумма) А 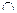 В есть множество всех элементов, принадлежащих А или В. Тогда
В есть множество всех элементов, принадлежащих А или В. Тогда 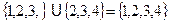
2. Пересечение (произведение) 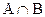 есть множество всех элементов принадлежащих одновременно как А, так и В. Тогда:
есть множество всех элементов принадлежащих одновременно как А, так и В. Тогда: 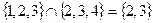 .
.
3. Разность А \ В есть множество, состоящее из всех элементов А, не входящих в В. Тогда: 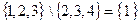 .
.
4. Дизъюнктивная сумма 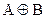 есть множество элементов, принадлежащих или А, или В (но не обоим вместе). Тогда
есть множество элементов, принадлежащих или А, или В (но не обоим вместе). Тогда 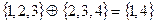 .
.
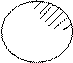
Задача 2. Дано: 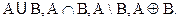 Требуется: использовать круги Эйлера для наглядного изображения соотношений между подмножествами А и В, составляющих универсум
Требуется: использовать круги Эйлера для наглядного изображения соотношений между подмножествами А и В, составляющих универсум 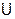 .
.
|
|
|
|












 1 2 3 4
1 2 3 4  | |||||||
 | |||||||
 | |||||||
 | |||||||

II. Векторная алгебра- это раздел математики, изучающий величины (векторы), которые характеризуются одновременно как числом (положительным, отрицательным, равным нулю), так и направлением в трехмерном (или двухмерном) пространстве.
Задача 9. Дано: координаты вершин пирамиды АВСD: А (2;1;0), В (3;-1;2), С (13;3;10), D (0;1;4). Требуется: 1) записать векторы 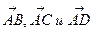 в системе орт i, j, k и найти модули этих векторов; 2) найти угол между векторами
в системе орт i, j, k и найти модули этих векторов; 2) найти угол между векторами 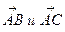 ; 3) найти проекцию вектора
; 3) найти проекцию вектора 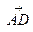 на вектор
на вектор 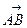 ; 4) найти площадь грани АВС; 5) найти объем пирамиды АВСD.
; 4) найти площадь грани АВС; 5) найти объем пирамиды АВСD.
Решение. 1. Произвольный вектор а может быть представлен в системе орт i, j, k следующей формулой:
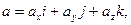 (1)
(1)
где ах, ау, аz – проекции вектора а на координатные оси Ох, Оу и Оz, а i, j, и k – единичные векторы, направления которых совпадают с положительным направлением осей Ох, Оу и Оz. Если даны точки М1 (х1;у1;z1) и М2 (х2;у2;z2), то проекции вектора 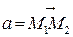 на координатные оси находятся по формулам:
на координатные оси находятся по формулам:
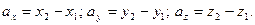 (2)
(2)
Тогда
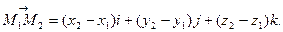 (3)
(3)
Подставив в (3) координаты точек А и В, получают вектор 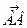 :
:
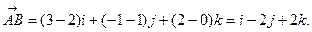
Аналогично, подставляя в (3) координаты точек А и С, находят
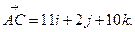
Подставив в (3) координаты точек А и D, находят вектор 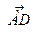 :
:
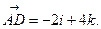
Если вектор а задан формулой (1), то его модуль вычисляется по формуле
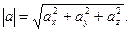 (4)
(4)
Применяя (4), получают модули найденных векторов:
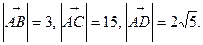
2. Косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей. Скалярное произведение векторов 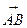 и
и 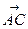 равно:
равно:
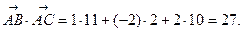
Модули этих векторов уже найдены: 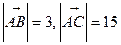 . Следовательно,
. Следовательно,
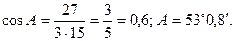
3. Проекция вектора 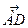 на вектор
на вектор 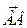 равна скалярному произведению этих векторов, деленному на модуль вектора
равна скалярному произведению этих векторов, деленному на модуль вектора 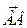 :
:
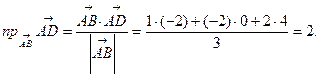
4. Площадь грани АВС равна половине площади параллелограмма, построенного на векторах 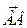 и
и 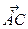 . Можно обозначить векторное произведение вектора
. Можно обозначить векторное произведение вектора 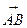 на вектор
на вектор 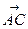 через вектор
через вектор 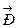 . Тогда, как известно, модуль вектора Р выражает собой площадь параллелограмма, построенного на векторах
. Тогда, как известно, модуль вектора Р выражает собой площадь параллелограмма, построенного на векторах 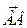 и
и 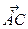 , площадь грани АВС будет равна половине модуля вектора Р:
, площадь грани АВС будет равна половине модуля вектора Р:
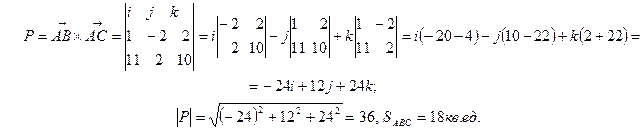
5. Объем параллелепипеда, построенного на трех некомпланарных (не лежат в одной плоскости) вектора, равен абсолютной величине их смешанного произведения.
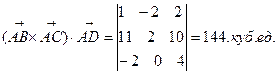
Следовательно, объем параллелепипеда равен 144 куб. ед., а объем заданной пирамиды АВСD равен 24 куб. ед.
III. Матрицы – это раздел дискретной математики, изучающий совокупности чисел или объектов другой природы, расположенных в виде прямоугольной таблицы.
Задача 10. Дано: система линейных уравнений:
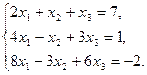 (1)
(1)
Требуется: 1).записать исходную систему линейных уравнений в матричной форме; 2). решить систему линейных уравнений с помощью обратной матрицы.
Решение. 1. Пусть А – матрица коэффициентов при неизвестных х1, х2, х3; Х – матрица-столбец неизвестных и Н – матрица-столбец из свободных членов:
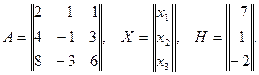
Левую часть системы (1) можно представить в виде произведения матриц А.Х, а правую – в виде матрицы Н. Следовательно, матричное уравнение
А.Х=Н. (2)
Если определитель матрицы А отличен от нуля, то матрица А имеет обратную матрицу А-1. В этом случае можно обе части равенства (2) умножить слева на матрицу А-1,
А-1.А.Х=А-1.Н.
Так как А-1.А=Е, где Е – единичная матрица, а Е.Н=Х, то матричная запись решения системы линейных уравнений будет иметь вид
Х= А-1.Н. (3)
2. Для нахождения обратной матрицы А-1 необходимо сначала найти определитель
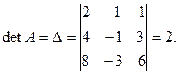
Тогда обратная матрица 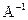 определяется путем последовательности трех шагов:
определяется путем последовательности трех шагов:
1) элементы матрицы А заменяются их алгебраическими дополнениями 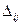 , т.е. определителями, полученными удалением из матрицы А S-й строки и K-го столбца, причём каждый определитель умножается еще на (-1)s+k:
, т.е. определителями, полученными удалением из матрицы А S-й строки и K-го столбца, причём каждый определитель умножается еще на (-1)s+k:
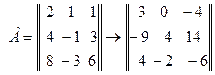
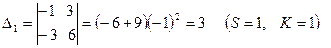
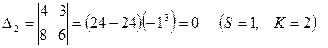
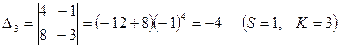
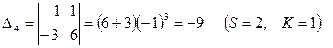
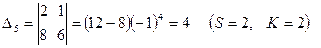
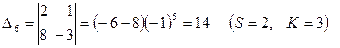
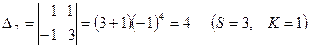
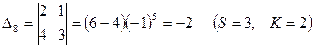
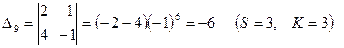
2) матрица алгебраических дополнений транспонируется, в результате чего получают взаимную (присоединенную) матрицу к А (Аdj A)
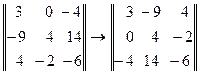
3) взаимная матрица, умножаемая на det A, и получают
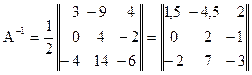
3. В соответствии с (3) можно записать
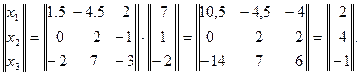
Следовательно, решение системы линейных уравнений х1= 2, х2 = 4, х3 = -1.
Задача 11. Дано: система линейныхравнений:
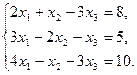
Требуется: 1) определить совместна ли исходная система линейных уравнений;
2) решить систему, если она совместна.
Решение. 1. Определение расширенной матрицы путем присоединения к матрице А (матрица, составленная из коэффициентов при неизвестных х1, х2, х3)
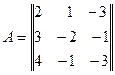 столбца свободных членов
столбца свободных членов 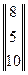 .
.
Тогда получают расширенную матрицу системы
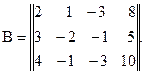
2. Определение рангов матриц А и В
2.1. Преобразование матрицы А по правилу: сумму элементов первых двух столбцов прибавить к соответствующим элементам третьего столбца
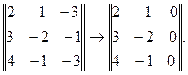
Анализ показывает, что определитель третьего порядка 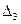 равен нулю, т.к. все элементы третьего столбца равны нулю. Определитель второго порядка
равен нулю, т.к. все элементы третьего столбца равны нулю. Определитель второго порядка 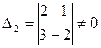 . Следовательно, ранг матрицы А равен 2, т.е. r(A) =2.
. Следовательно, ранг матрицы А равен 2, т.е. r(A) =2.
2.2. Первое преобразование матрицы В по правилу: сумму элементов первых двух столбцов прибавить к соответствующим элементам третьего столбца
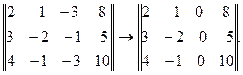
Тогда все элементы третьего столбца равны нулю.
Второе преобразование матрицы В по правилу: элементы первого столбца умножить на –3, второго на –2 и их сумму вычесть из соответствующих элементов четвертого столбца
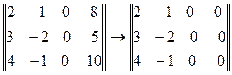
Так как элементы двух последних столбцов равны нулю, то все определители третьего порядка матрицы В раны нулю и, следовательно, ранг матрицы В равен 2, т.е. r(В) =2.
Вывод: система линейных уравнений совместна, т.к. выполнено необходимое и достаточное условие r(A) = r(В) =2.
3. Поскольку ранг матриц А и В равны 2, а система содержит 3 неизвестных, то она имеет бесконечное число решений. Пусть выбран базисный определитель 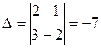 , а в качестве базисных неизвестных х1 и х2. Составляется подсистема, состоящая из первых двух уравнений заданной системы, и свободное неизвестное х3 переносят в правую часть
, а в качестве базисных неизвестных х1 и х2. Составляется подсистема, состоящая из первых двух уравнений заданной системы, и свободное неизвестное х3 переносят в правую часть
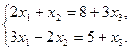
4. Решая подсистему относительно базисных неизвестных х1 и х2, находят х1=3+х3, х2=2+х3. Полученное решение называется общим. Конкретные решения получают задавшись х3. Например, пусть х3 =-2, тогда х1 =1, х2 =0.
IV. Функциональный анализ – это раздел математики, изучающий свойства операторов, действующих между любыми (главным образом функциональными) пространствами. Основными понятиями функционального анализа являются: предел, функция, производная.
Задача 12. Дано: четыре математические выражения:
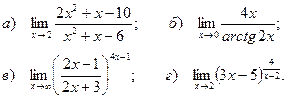
 Требуется: найти пределы этих выражений при условии, что
Требуется: найти пределы этих выражений при условии, что
а) 
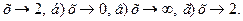
Решение. 1. Непосредственная подстановка предельного значения аргумента х =2 приводит к неопределенности вида 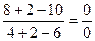 .
.
Для раскрытия неопределенности необходимо:
- разложим числитель и знаменатель дроби на множители
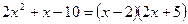 и
и 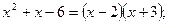
- сократить дробь на общий множитель (х-2).
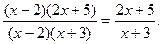
Тогда
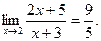
2. Пусть arctg 2x=y. Тогда 2х=tg y и очевидно, что если х®0, то y®0.
Следовательно,
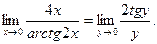
Используя первый замечательный предел, можно осуществить следующее преобразование
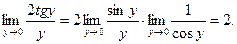
Существует второй способ нахождения предела на основе того, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной. Так как при х®0 arctg 2x~2х, то
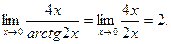
3. При х®¥ основание 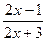 стремиться к 1, а показатель степени 4х+1 стремиться к бесконечности. Следовательно, имеет место неопределенность вида 1 ¥. Для раскрытия неопределенности следует представить основание в виде суммы 1 и некоторой бесконечно малой величины
стремиться к 1, а показатель степени 4х+1 стремиться к бесконечности. Следовательно, имеет место неопределенность вида 1 ¥. Для раскрытия неопределенности следует представить основание в виде суммы 1 и некоторой бесконечно малой величины
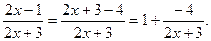
Тогда
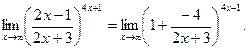
Пусть 2х+3=-4у; следовательно при х®+¥ переменная у® -¥. Показатель степени можно выразить через новую переменную у. Так как 2х=-4у-3, то 4х+1=-8у-5.
Таким образом,
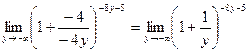 .
.
Используя второй замечательный предел, можно осуществить следующее преобразование
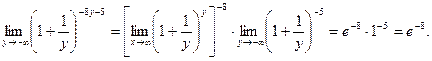
4. При х®2 основание (3х-5) стремится к единице, а показатель степени 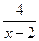 стремиться к бесконечности.
стремиться к бесконечности.
Пусть 3х-5=1+a, где a®0 при х®2. Тогда 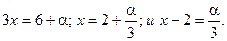
Выразив основание и показатель степени через a, получают
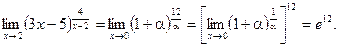
При этом используют известные выражения
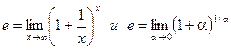
Задача 13. Дано: функция у задана различными аналитическими выражениями для различных областей изменения аргумента х
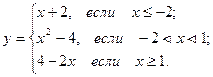
Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти предел функции у при приближении аргумента х к точке разрыва слева и справа; 3) найти скачок функции в точке разрыва; 4) построить график данной функции y = f(x).
Решение. 1. Данная функция определена и непрерывна в интервалах (- ¥, -2), (-2, 1) и (1, + ¥). При х =-2 и х =1 меняется аналитическое выражение функции, и только в этих точках функция может иметь разрыв.
2. Односторонние пределы в функции в точке х = - 2 равны:
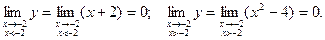
Односторонние пределы совпадают. Функция в этой точке непрерывна.
3. Односторонние пределы функции в точке х =1 равны:
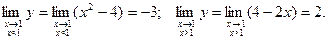
Односторонние пределы функции у в точке х =1 не равны между собой, в этой точке функция имеет разрыв первого рода.
4. Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельным значениями. Следовательно, в точке х =1 скачок функции 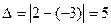 .
.
5. График функции y = f(x)
 |
-2
-4
Задача 14. Дано: функция 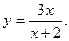 и значения аргумента х1 = -2 и х2 = 3
и значения аргумента х1 = -2 и х2 = 3
Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва;
3) построить график данной функции на отрезке [-6;6].
Решение. Если ищется предел функции у=f(х) при условии, что аргумент х, стремясь к своему предельному значению a, может принимать только такие значения, которые меньше a, то этот предел, если он существует, называется правосторонним (правым) пределом данной функции в точке х=a и условно обозначается так:
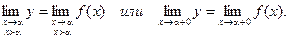
1. Функция у=f(х) непрерывна при х=a, если выполняются следующие условия: 1) функция у=f(х) определена не только в точке a, но и в некотором интервале, содержащем эту точку;
2) функция у=f(х) имеет при х®a конечные и равные между собой односторонние пределы;
3) односторонние пределы при х®a совпадают со значением функции в точке a, т.е.
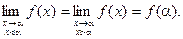
Если для данной функции у=f(х) в данной точке х=a хотя бы одно из перечисленных трех условий не выполняется, то функция называется разрывной в точке х=a.
Разрыв функции у=f(х) в точке х=a называется разрывом первого рода, если односторонние пределы слева и справа существуют, но не равны между собой. Если же хотя бы один из односторонних пределов не существует, разрыв в этой точке называется разрывом второго рода.
2. При х1 = -2 данная функция 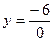 не существует: в этой точке функция терпит разрыв.
не существует: в этой точке функция терпит разрыв.
3. Односторонние пределы функции при х1 ® -2 слева и справа
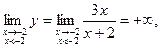
так как знаменатель стремится к нулю, оставаясь отрицательным;
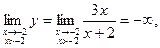
так как знаменатель стремится к нулю, оставаясь положительным.
Следовательно, при х = -2 данная функция имеет разрыв второго рода.
4. При х =3 данная функция 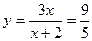 т.е. она в этой точке непрерывна, так как выполняются все три условия непрерывности функции.
т.е. она в этой точке непрерывна, так как выполняются все три условия непрерывности функции.
5. График функции имеет вид:
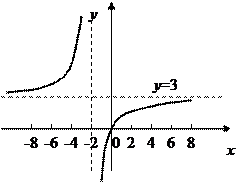 |
Задача 15. Дано: функции вида:
1) 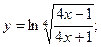 2)
2) 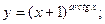
3) 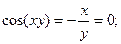 4)
4) 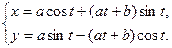
Требуется: найти производные 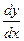 функций
функций
Решение. 1. Пользуясь правилом логарифмирования корня и дроби, можно преобразовать правую часть
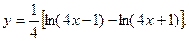
Применяя правила и формулы дифференцирования, получают:
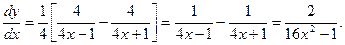
2. Осуществляют логарифмирование по основанию обеих частей равенства
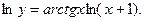
Дифференцируют обе части равенства, считая ln у сложной функцией от переменной х
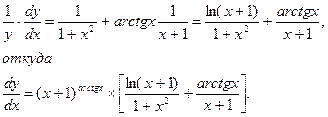
3. В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную 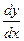 , необходимо дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной
, необходимо дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной 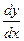 =y1.
=y1.
Дифференцируя обе части исходного уравнения, находят:
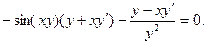
Из полученного равенства, связывающего х, у и 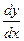 , находим производную путем преобразований:
, находим производную путем преобразований:
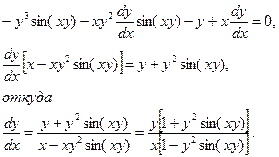
4. Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти искомую производную, необходимо предварительно найти дифференциалы dx и dy и затем взять их отношение
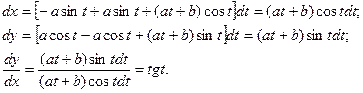
V. Дифференциальное исчисление - это раздел математики, исследующий операции нахождения производных функций. Основными понятиями дифференциального исчисления являются: дифференциал, правила дифференцирования функций, производные n-го порядка.
Задача 16. Дано: функции вида: а) 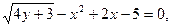 б)
б) 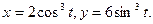
Требуется: найти производные второго порядка этих функций
Решение. а) Функция у задана в неявном виде Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:
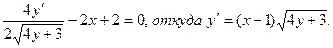 (1)
(1)
Снова дифференцируем по х обе части (1):
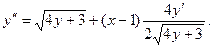 (2)
(2)
Заменив у’ в (2) правой частью (1), получим
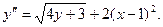
б) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти производную у’, находим сперва дифференциалы dy и dx и затем берем отношение этих дифференциалов:
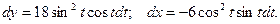
Тогда
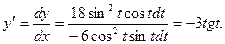
Производная второго порядка 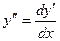 . Следовательно, чтобы найти у’’, надо найти дифференциал dy’:
. Следовательно, чтобы найти у’’, надо найти дифференциал dy’:
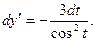
Тогда
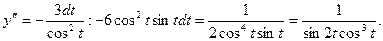
Задача 17. Дано: функция 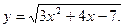 Требуется: найти приближенное значение функции при х2=5,85, исходя из её точного значения при х1 = 6
Требуется: найти приближенное значение функции при х2=5,85, исходя из её точного значения при х1 = 6
Решение. Известно, что дифференциал dy функции у=f(х) представляет собой главную часть приращения этой функции Dу. Если приращение аргумента Dх мало по абсолютной величине, то Dу приближенно равно дифференциалу, т.е. Dу»dy. Так как Dу=f(x+Dx)-f(x), а dy=f(x)dx, то имеет место приближенное равенство:
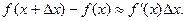
Пусть х=х1, х+Dх=х2, т.е. Dх=х2-х2.
Тогда
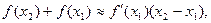
или
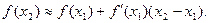 (1)
(1)
Приближенное равенство (1) дает возможность найти значение функции при х=х2, если известно значение функции и ее производной при х=х1.
Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f’(x) при х =6:
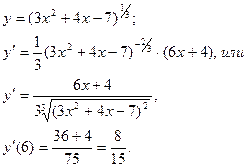
Применяя (1), получаем
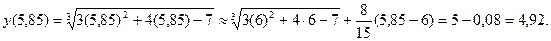
Задача 18. Дано: величина tg 470. Требуется: найти приближенное значение величины.
Решение. Применяем формулу
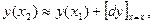
Рассмотрим функции у=tgx. Дифференциал 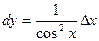 . Так как tg 450=1, то положим х1 =450 и х2 =470. Приращение Dх =470-450=20, или в радианном измерении
. Так как tg 450=1, то положим х1 =450 и х2 =470. Приращение Dх =470-450=20, или в радианном измерении 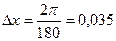 . Следовательно,
. Следовательно,
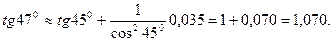
VI. Интегральное исчисление - это раздел математики, исследующий способы определения функции по заданному дифференциалу или производной (задача, обратная задаче дифференциального исчисления). Основными понятиями интегрального исчисления являются: первообразная функция, неопределенный интеграл, определенный интеграл.
Дифференциальные уравнения - это раздел математики, изучающий уравнения, связывающие между собой независимую переменную х, искомую функцию y и её производные различных порядков по х. Основными понятиями этого раздела математики являются: дифференциальные уравнения первого и второго порядка, дифференциальные уравнения второго порядка с постоянными коэффициентами.
Задача 19. Дано: определенный интеграл
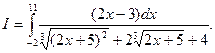
Требуется: вычислить интеграл.
Решение. Делают подстановку. Пусть 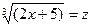 . Тогда 2х+5=z3; 2dx=3z3dz; dx=3/2z2dz. Определяют пределы интегрирования для переменной z. При х =-2 получают z =1, при х =11 получают z = 3.
. Тогда 2х+5=z3; 2dx=3z3dz; dx=3/2z2dz. Определяют пределы интегрирования для переменной z. При х =-2 получают z =1, при х =11 получают z = 3.
Выразив подынтегральное выражение через z и переходя к новым пределам получают
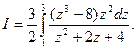
Так как разность кубов 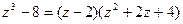 , то сократив на знаменатель, получают
, то сократив на знаменатель, получают
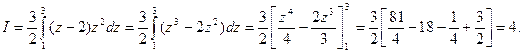
Задача 20. Дано: уравнение эллипса:
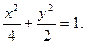 (1)
(1)
Требуется: вычислить площадь поверхности эллипсоида, полученного вращением вокруг оси Ох эллипса.
Решение. Площадь поверхности, образованной вращением вокруг оси Ох дуги кривой y=f(x) между точками с абсциссами х=а и х=b, вычисляется по формуле
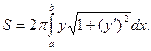 (2)
(2)
Из уравнения эллипса (1) находят 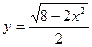 . Производная
. Производная 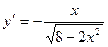 . Используя формулу (2), получают
. Используя формулу (2), получают
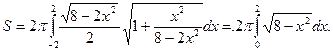
Чтобы вычислить последний интеграл, пологают 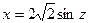 . Тогда z =0 при х =0 и z =p/4 при х =2 и площадь поверхности эллипсоида.
. Тогда z =0 при х =0 и z =p/4 при х =2 и площадь поверхности эллипсоида.
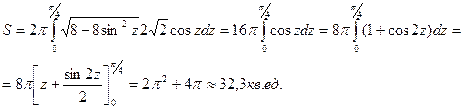
Задача 21. Дано: определенный интеграл 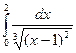 . Требуется: вычислить интеграл или установить его расходимость.
. Требуется: вычислить интеграл или установить его расходимость.
Решение. Подынтегральная функция 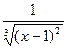 имеет бесконечный разрыв при х =1, т.е. в точке, принадлежащей интервалу интегрирования. Данный интеграл является несобственным. Если подынтегральная функция f(x) интеграла
имеет бесконечный разрыв при х =1, т.е. в точке, принадлежащей интервалу интегрирования. Данный интеграл является несобственным. Если подынтегральная функция f(x) интеграла 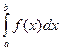 имеет бесконечный разрыв при х=с, где а<с<b, а во всех других точках отрезка [ a,b ]непрерывна, то по определению полагают:
имеет бесконечный разрыв при х=с, где а<с<b, а во всех других точках отрезка [ a,b ]непрерывна, то по определению полагают:
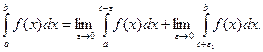 (*)
(*)
Если оба предела в правой части(*) существуют, то интеграл 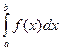 называется сходящимся. Если хотя бы один из указанных пределов не существует, то интеграл
называется сходящимся. Если хотя бы один из указанных пределов не существует, то интеграл 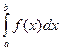 называется расходящимся.
называется расходящимся.
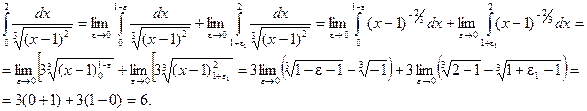
Следовательно, данный интеграл – сходящийся.
Замечание. Равенство (*) можно использовать для каждой отдельной точки разрыва, принадлежащей интервалу (a,b).
Задача 22. Дано: уравнение 2хуdx+(y2-x2)dy=0.
Требуется: найти общее решение уравнения.
Решение. Данное уравнение является однородным, так как коэффициенты при dx и dy суть однородные функции одного и того же измерения (второго) относительно переменных х и у. Применяют подстановку у=хt, где t – некоторая функция аргумента х.
Если у=хt, то дифференциал dy=d(xt)=tdx+xdt, и данное уравнение примет вид
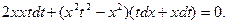
Сократив на х2, получают:
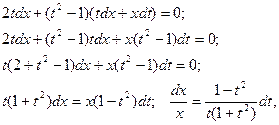
то есть уравнение с разделенными переменными относительно х и t. Интегрируя, находят общее решение этого уравнения:
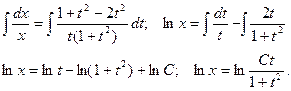
Потенцируя, находят 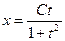 , или
, или 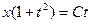 . Из введенной подстановки следует, что
. Из введенной подстановки следует, что 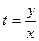 . Следовательно,
. Следовательно, 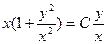 или
или 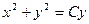 - общее решение данного уравнения.
- общее решение данного уравнения.
Задача 23. Дано: уравнение 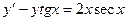 . Требуется: найти общее решение уравнения.
. Требуется: найти общее решение уравнения.
Решение. Данное уравнение является линейным, так как оно содержит искомую функцию у и ее производную у’ в первой степени и не содержит их произведений.
Применяют подстановку у=uv, где u и v – некоторые неизвестные функции аргумента х. Если у=uv, то y’=(uv)’=u’v+uv’ и данное уравнение примет вид
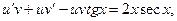
или
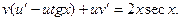 (1)
(1)
Так как искомая функция у представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберают функцию u так, чтобы выражение, стоящее в круглых скобках левой части равенства (1), обращалось в нуль, т.е. выбирают функцию u так, чтобы имело место равенство
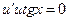 (2)
(2)
При таком выборе функции u уравнение (1) примет вид
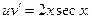 (3)
(3)
Уравнение (2) есть уравнение с разделяющимися переменными относительно u и х. Решение этого уравнения:
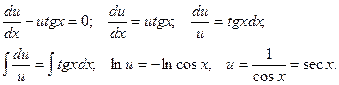
Чтобы равенство(2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находят то частное решение, которое соответствует значению произвольной постоянной С=0. Подставив в (3) найденное выражение для u, получают: 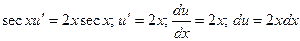 . Интегрируя, получают
. Интегрируя, получают 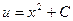 . Тогда
. Тогда 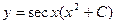 - общее решение данного уравнения.
- общее решение данного уравнения.
Задача 24. Дано: уравнение: 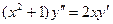 . Требуется: найти частное решение, удовлетворяющее начальным условиям: у (0)=1; у’ (0)=3.
. Требуется: найти частное решение, удовлетворяющее начальным условиям: у (0)=1; у’ (0)=3.
Решение. Данное дифференциальное уравнение второго порядка не содержит явно функцию у. Полагают у’ = р, где р – некоторая функция аргумента х. Если у’ = р, то 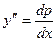 и данное уравнение примет вид
и данное уравнение примет вид 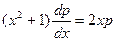 . Получают уравнение первого порядка относительно переменных р и х. Решение этого уравнения:
. Получают уравнение первого порядка относительно переменных р и х. Решение этого уравнения:
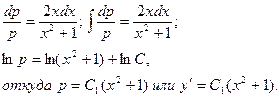
Определяют численное значение С1 при указанных начальных условиях. Имеем 3=С1(0+1). Следовательно, С1 =3. Теперь решают уравнение первого порядка 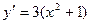 :
:
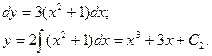
Определяют численное значение С2 при указанных начальных условиях. Имеют 1=0+0+С2; С2 =1.
Таким образом, 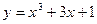 есть частное решение, удовлетворяющее указанным начальным условиям.
есть частное решение, удовлетворяющее указанным начальным условиям.
Задача 25. Дано: уравнение 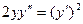 . Требуется: найти частное решение, удовлетворяющее начальным условиям: у (-1)=4; у’ (-1)=1.
. Требуется: найти частное решение, удовлетворяющее начальным условиям: у (-1)=4; у’ (-1)=1.
Решение. Данное уравнение второго порядка не содержит явно аргумента х. Полагают у’ = р, где р – некоторая функция переменной у. Если у’ = р, то 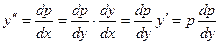 . Тогда данное уравнение примет вид
. Тогда данное уравнение примет вид
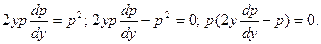
Если приравнять нулю первый множитель, то получают: р =0; у’ =0; у=С – решение данного уравнения.
Приравнивая нулю второй множитель:
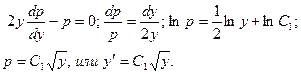
Используя начальные условия, находят С1:
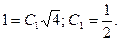
Далее решают уравнение 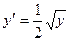 :
:
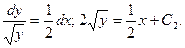
Теперь определяют значение С2:
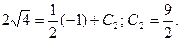
Тогда
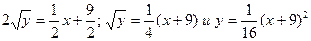
- искомое частное решение, удовлетворяющее указанным начальным условиям.
Задача 26. Дано: система уравнений
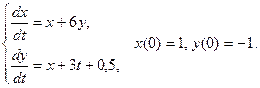
Требуется: решить систему уравнений и выделить частные решения, удовлетворяющие заданным начальным условиям:
Решение. Обе части первого уравнения системы дифференцируют по переменной t:
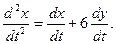
В полученном уравнении заменяют 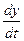 правой частью второго уравнения системы. В результате получают однородное линейное уравнение второго порядка:
правой частью второго уравнения системы. В результате получают однородное линейное уравнение второго порядка:
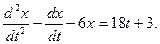 (1)
(1)
Составляют и решают соответствующее однородное линейное уравнение:
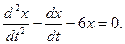 (2)
(2)
Характеристическое уравнение k2-k-6=0 имеет корни: k1 =-2, k2 =3. Следовательно, общее решение (2) имеет вид
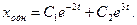
Находят частное решение х=Аt+В. Дважды дифференцируя, получяют (х)'=А, (х)’’=0. Подставив в (1), находят А =-3 и В =0. Следовательно, х=-3t и
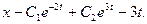 (3)
(3)
Из первого уравнения системы находят, что 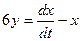 , или
, или 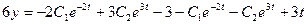 , откуда
, откуда
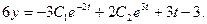 (4)
(4)
Подставив начальные условия в (3) и (4), получают систему
С1+С2=1 и 3С1-2С2=3.
Решение этой системы дает С1 =1 и С2 =0. Следовательно,
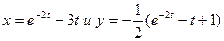
- частные решения, удовлетворяющие заданным начальным условиям.
VII. Аналитическая геометрия на плоскости - это раздел математики, изучающий способы решения двух видов задач:
- дана линия, рассматриваемая как множество точек, требуется составить уравнение этой линии,
- дано уравнение некоторой линии, требуется изучить по этому уравнению её геометрические свойства (форму и расположение).
Основными понятиями этого раздела являются: прямоугольная и полярная системы координат, уравнение линии, прямая линия, линии второго порядка.
Задача 27. Дано: координаты вершин треугольника АВС: А (4; 3), В (16; -6), С (20; 16). Требуется: найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты СD и ее длину; 5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой CD; 6)уравнение прямой, проходящей через точку К параллельно стороне АВ; 7) координаты точки М, расположенной симметрично точке А относительно прямой CD.
Решение. 1. Расстояние d между точками A (x1; y1) и B (x2; y2) определяется по формуле
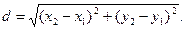 (1)
(1)
Применяя (1), находят длину стороны АВ:
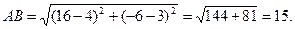
2. Уравнение прямой проходящей через точки А (x1; y1) и B (x2; y2), имеет вид
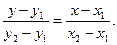 (2)
(2)
Подставляя в (2) координаты точек А и В, получают уравнение стороны АВ:
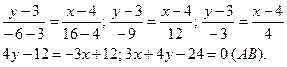
Решив последнее уравнение относительно y, находят уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:
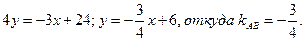
Подставив в (2) координаты точек В и С, получают уравнение прямой ВС:
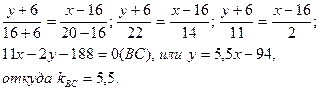
3. Известно, что тангенс угла j между двумя прямыми, угловые коэффициенты, которых соответственно равны k1 и k2, вычисляется по формуле
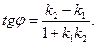 (3)
(3)
Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых найдены: kAB =-¾; kВС =5,5. Применяя (3), получают
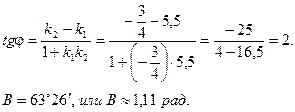
4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид
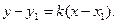 (4)
(4)
Высота CD перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты CD, используют условие перпендикулярности прямых. Так как kAB =-¾, то kCD = 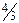 . Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получают
. Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получают
Чтобы найти длину высоты UD, определяют сперва координаты точки D – точки пересечения прямых АВ и CD. Решая совместно систему
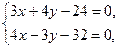
находят 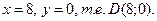
По формуле (1) находят длину высоты CD:
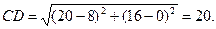
5. Чтобы найти уравнение медианы АЕ, определяют сначала координаты точки Е, которая является серединой стороны ВС, применяя формулы деления отрезка на две равные части:
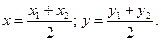 (5)
(5)
Следовательно,
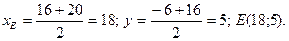
Подставив в (2) координаты точек А и Е, находят уравнение медианы:
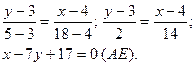
Чтобы найти координаты точки пересечения высоты CD и медианы АЕ, решают совместно систему уравнений
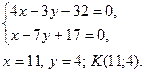
6. Так как искомая прямая параллельная стороне АВ, то ее угловой коэффициент будет равен угловому коэффициенту прямой АВ. Подставив в (4) координаты найденной точки К и угловой коэффициент k =-¾, получают
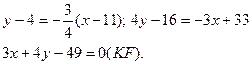


Рис. 1. Рис. 2
7. Так как прямая АВ перпендикулярна прямой CD, то искомая точка М, расположенная симметрично точке А относительно прямой CD, лежит на прямой АВ. Кроме того, точка D является серединой отрезка АМ. Применяя формулы (5), находят координаты искомой точки М:
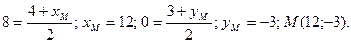
Треугольник АВС, высота CD, медиана АЕ, прямая KF и точка М построены в системе координат хОy на рис. 1.
Задача 28. Дано: геометрическое место точек, отношение расстояний которых до данной точки А (4;0) и до данной прямой х =1 равно 2. Требуется: составить уравнение геометрического места точек
Решение. В системе координат xOy строят точку А (4;0) и прямую х=1. Пусть М (x;y) – произвольная точка искомого геометрического места точек. Опускают перпендикуляр МВ на данную прямую х =1 и определяют координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно В (1; y) (рис. 2).
По условию задачи МА:МВ =2. Расстояния МА и МВ находят по формуле (1) задачи 27:
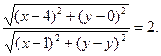
Возведя в квадрат левую и правую части, получают
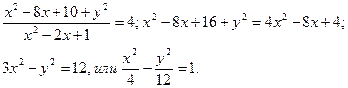
Полученное уравнение представляет собой гиперболу, у которой действительная полуось а =2, а мнимая 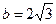 .
.
Определяют фокусы гиперболы. Дли гиперболы выполняется равенство 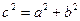 . Следовательно,
. Следовательно, 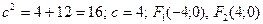 – фокусы гиперболы. Как видно, заданная точка А (4;0) является правым фокусом гиперболы.
– фокусы гиперболы. Как видно, заданная точка А (4;0) является правым фокусом гиперболы.
Определяют эксцентриситет полученной гиперболы:
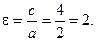
Уравнения асимптот гиперболы имеют вид 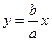 и
и 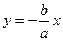 . Следовательно,
. Следовательно, 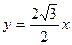 , или
, или 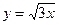 и
и 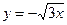 – асимптоты гиперболы. Прежде чем построить гиперболу, строят ее асимптоты.
– асимптоты гиперболы. Прежде чем построить гиперболу, строят ее асимптоты.
Задача 29. Дано: геометрическое место точек, равноудаленных от точки А (4;3) и прямой y =1. Требуется: составить уравнение геометрического места точек.
Решение. Пусть М (х;у) – одна из точек искомого геометрического места точек. Опускают из точки М перпендикуляр МВ на данную прямую у =1 (рис. 3). Определяем координаты точки В. Очевидно, абсцисса точки В равна абсциссе точки М, а ордината точки В равна 1, т.е. В (х; 1). По условию задачи МА = МВ. Следовательно, для любой точки М (х;у), принадлежащей искомому геометрическому месту точек, справедливо равенство:
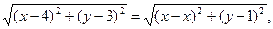
или
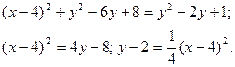
Полученное уравнение определяет параболу с вершиной в точке О’ (4;2). Чтобы уравнение параболы привести к простейшему виду, считают х -4= Х и у +2= Y; тогда уравнение параболы принимает вид: Y = ¼ Х 2(*).
Чтобы построить найденную кривую переносят начало координат в точку О’ (4;2), строят новую систему координат ХО’Y оси которой соответственно параллельны осям Ох и Оy, и затем в этой новой системе строят параболу (*) (рис. 3).


Рис. 3. Рис. 4
Задача 30. Дано: гипербола, фокусы которой расположены на оси абсцисс, если она проходит через точки А (-8;12), В (12; 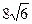 ). Требуется: 1). составить каноническое уравнение гиперболы; 2). найти все точки пересечения этой гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы.
). Требуется: 1). составить каноническое уравнение гиперболы; 2). найти все точки пересечения этой гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы.
Решение. Каноническое уравнение гиперболы имеет вид
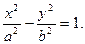
По условию точки А и В лежат на гиперболе. Следовательно, координаты этих точек удовлетворяют уравнению (1). Подставив в уравнение (1) вместо текущих координат х и у координаты точек А и В, получают систему двух уравнений относительно неизвестных а и b:
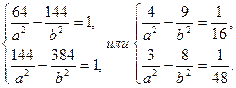
Решая систему, получаают: а2 =16, b2 =48.
Таким образом, уравнение искомой гиперболы 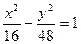 . Определяют фокусы этой гиперболы. Так как с2=а2+b2 =16+48=64; то с= 8; F1 (-8;0), F2 (8;0).
. Определяют фокусы этой гиперболы. Так как с2=а2+b2 =16+48=64; то с= 8; F1 (-8;0), F2 (8;0).
Уравнение окружности, проходящей через начало координат, имеет вид
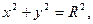
где R – радиус окружности.
Так как по условию окружность проходит через фокусы гиперболы, то R=c= 8. Следовательно, 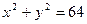 - уравнение окружности. Чтобы найти точки пересечения гиперболы с окружностью, решают систему уравнений
- уравнение окружности. Чтобы найти точки пересечения гиперболы с окружностью, решают систему уравнений
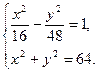
В результате получают 4 точки пересечения: М1 (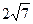 ;6), М2 (-
;6), М2 (- 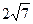 ;6), М3 (-
;6), М3 (- 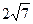 ;-6), М4 (
;-6), М4 (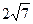 ;-6) (рис. 4).
;-6) (рис. 4).
ВАРИАНТЫ ЗАДАЧ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
 2015-03-22
2015-03-22 1230
1230
