|

Каждому решению x1 + ××× +xn = k соответствует неубывающая последовательность y1 ≤y2 ≤ × × × ≤yn-1, где y1=x1, y2 = y1+x2, ×××, yn-1 = yn-2 + xn-1.
Теорема 7. 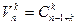 .
.
Доказательство. Рассмотрим график неубывающей функции
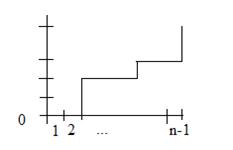
Рис. 2.3. График неубывающей функции
График задается последовательностью из 0 и 1
0 0 1 1 0 0 … 0 1 0 0 … 1 1 … 1
состоящей из n-1+k разрядов, имеющих k единиц.
Следствие 1. 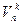 равно числу неубывающих функций {1,2, ×××, k } ® {1,2, ×××, n }.
равно числу неубывающих функций {1,2, ×××, k } ® {1,2, ×××, n }.
Доказательство. Первый способ: транспонировать графики.
Второй способ: число неубывающих функций k ® n равно
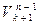 =
= 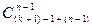 =
= 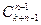 .
.
Получаем следующую таблицу, содержащую числа конфигураций
| функций m®n | неубывающих функций m®n | |
| Всех | nm | 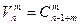
|
| Инъективных | 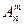
| 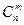
|
| Сюръективных | ? | 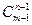
|
| Биективных | n!, если m=n, иначе 0 | 1, если m=n, иначе 0 |
Здесь m = {0,1, ×××, m-1}. Например, число сюръективных функций
{0,1, ×××, m-1} ® {0,1, ×××, n-1}
равно 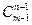 .
.
 2015-03-07
2015-03-07 312
312








