2015-03-07
412
Теорема 1. Число сочетаний удовлетворяет соотношениям:
; 
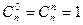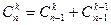(при 0 < k < n).
Доказательство. Число сочетаний, не содержащих n-й элемент, равно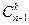 
, а содержащих – 
.
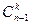Следующая таблица строится на основе теоремы 1 и называется треугольником Паскаля:
| n k | ||||||
Теорема 2. Число сочетаний из n по k равно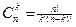 
.
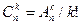Доказательство. По индукции по n. Или, сопоставляя каждой инъекции ее образ и учитывая, что число инъекций с одинаковым образом равно k!, получаем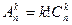 
Þ .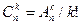
Теорема 3.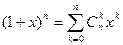 
(Бином Ньютона).
Доказательство. По индукции по n. Можно предложить также другое доказательство: Рассмотрим произведение n сомножителей (1+x) (1+x) × × × (1+x). Сомножители будем рассматривать как ящики. Произведение равно сумме степеней xk, причем при каждом k слагаемые xk получаются выбором из ящиков k элементов, равных x. Отсюда коэффициент при xk будет равен количеству содержащих k элементов подмножеств множества, состоящего из n элементов.
