Решение. 1 шаг. Уравнение равносильно следующему равенству

1 шаг. Уравнение равносильно следующему равенству

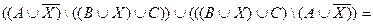Æ.

Пользуясь формулой 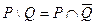, приходим к уравнению

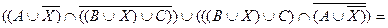Æ

С помощью правил де Моргана 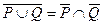и соотношения 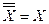преобразуем это уравнение к следующему

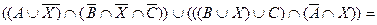Æ.

2 шаг. Обозначим операцию объединения Èзнаком сложения, а операцию пересечения Ç - знаком умножения. Получим уравнение

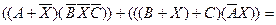Æ

Преобразуем его с помощью закона дистрибутивности (P+Q)R=PR+QR. Приходим к уравнению

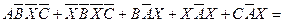Æ

Равенства 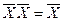и XX = X, вместе с соотношениям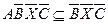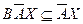и , и 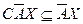приводят к уравнению

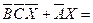Æ

3 шаг. Полученное уравнение равносильно системе двух уравнений

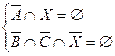
Из первого уравнения получаем 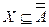, а из второго 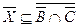. Эти соотношения приводят к соотношениям включения .

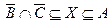Ответ: 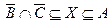, при условии .

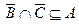Задача 2. Задано отношение R на множестве E = {1, 2, 3, 4, 5} с помощью матрицы (r_ij), где

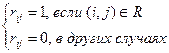
Представить данное отношение с помощью ориентированного графа, вершинами которого являются элементы множества E. Вершины i и j соединяются стрелкой, если .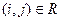

Выписать матрицы, соответствующие отношениям

1) R^-1 ,

2) RºR,

3) RÇ R^-1.

Является ли это отношение R

1) рефлексивным

2) иррефлексивным

3) симметричным

4) антисимметричным

5) транзитивным

6) отношением порядка

7) отношением эквивалентности

Варианты

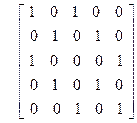
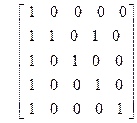
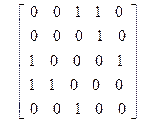
1)	2)	3)	4)
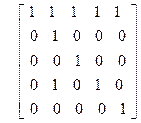
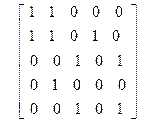
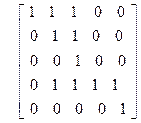
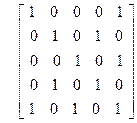
5)	6)	7)	8)
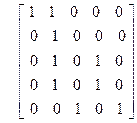
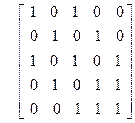
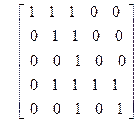
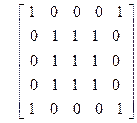
9)	10)	11)	12)
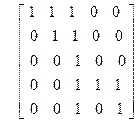
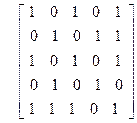
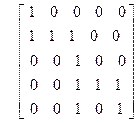
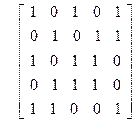
13)	14)	15)	16)
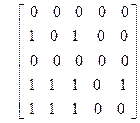
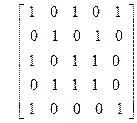
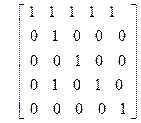
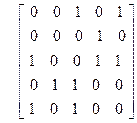
17)	18)	19)	20)
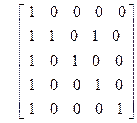
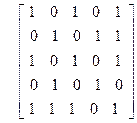
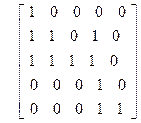
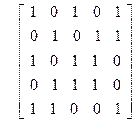
21)	22)	23)	24)
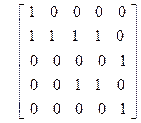
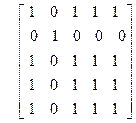
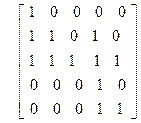
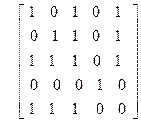
25)	26)	27)	28)
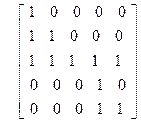
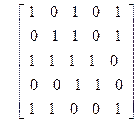
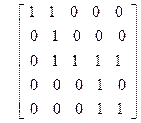
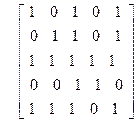
29)	30)	31)	32)
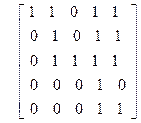
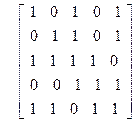
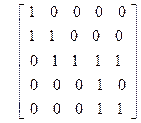
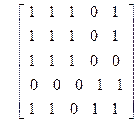
33)	34)	35)	36)

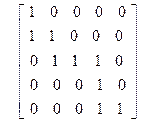
Пример решения задачи 2.

Выполнить действия, указанные в условии задачи 2, если отношение R на множестве E = {1, 2, 3, 4, 5} задано с помощью матрицы

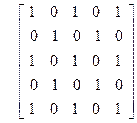
имеющей коэффициенты r_ij = 1 при (i,j)ÎR, и r_ij = 0 в других случаях.

Решение.

Представим отношение с помощью ориентированного графа, с множеством вершин E={1, 2, 3, 4, 5}. Вершины i и j соединяются стрелкой, если .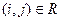

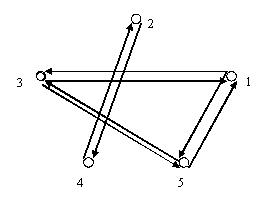
Рис. 1. Ориентированный граф, соответствующий отношению R

Выпишем матрицы

R^-1 = 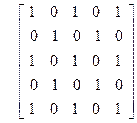, RÇ R^-1 = ,

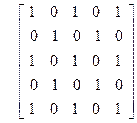R°R = =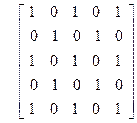

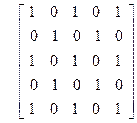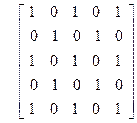
Ответим на вопросы:

Рефлексивность выполняется, поскольку r_ii=1 влечет (i,i)ÎR, для всех iÎE.

Иррефлексивность не выполняется, так как существуют iÎE, для которых (i,i)ÎR.

(например i=1).

Симметричность имеет место, ибо для всех i, j ÎE выполнено r_ij= r_ji.

Антисимметричность не выполняется, так как (1,3)ÎR и (3,1)ÎR, но 1¹3.

Транзитивность вытекает из R°R Í R.

Отношение не является отношением порядка, ибо оно не антисимметрично.

Отношение является отношением эквивалентности, поскольку оно рефлексивно, симметрично и транзитивно.