2.1 Оптимизация плана производства
В данном разделе показаны возможности использования модели линейного программирования (ЛП) для определения плана производства. Рассматривается задача производственного планирования, учитывающая динамику спроса, производства и хранения продукции. Наиболее часто такого рода задачи возникают на уровне агрегированного планирования и оперативного управления микроэкономическими объектами.
Постановка задачи:
Необходимо определить план производства одного или нескольких видов продукции, который обеспечивает наиболее рациональное использование имеющихся материальных, финансовых и других видов ресурсов. Такой план должен быть оптимальным с точки зрения выбранного критерия – максимума прибыли, минимума затрат на производство и т. д.
Введем обозначения:
n - количество выпускаемых продуктов;
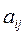 m - количество используемых производственных ресурсов (например, производственные мощности, сырье, рабочая сила);
m - количество используемых производственных ресурсов (например, производственные мощности, сырье, рабочая сила);
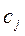 - объем затрат i -го ресурса на выпуск единицы j -й продукции;
- объем затрат i -го ресурса на выпуск единицы j -й продукции;
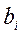 - прибыль от выпуска и реализации единицы j -го продукта;
- прибыль от выпуска и реализации единицы j -го продукта;
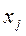 - количество имеющегося i -го ресурса;
- количество имеющегося i -го ресурса;
- объем выпуска j -го продукта
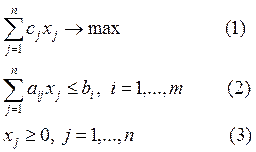 Формально задача оптимизации производственной программы может быть описана с помощью следующей модели линейного программирования:
Формально задача оптимизации производственной программы может быть описана с помощью следующей модели линейного программирования:
Здесь (1) – целевая функция (максимум прибыли);
(2) – система ограничений на объем имеющихся ресурсов;
(3) – ограничения на неотрицательность переменных.
Пример 1. Для изготовления трехвидов изделий A, B и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице 1. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида.
| Тип оборудования | Затраты времени (станко-ч) на обработку одного изделия вида | Общий фонд рабочего времени оборудования (ч) | ||
| А | В | С | ||
| Фрезерное | ||||
| Токарное | ||||
| Сварочное | ||||
| Шлифовальное | ||||
| Прибыль (руб.) |
Требуется определить, сколько изделий и какого вида требуется изготовить, чтобы прибыль от их реализации была максимальной. Составить математическую модель задачи.
Решение. Предположим, что будет изготовлено 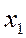 единиц изделий А,
единиц изделий А, 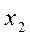 единиц изделий В и
единиц изделий В и 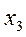 единиц изделий С. Тогда для производства такого количества изделий потребуется затратить
единиц изделий С. Тогда для производства такого количества изделий потребуется затратить 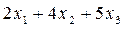 станко-часов фрезерного оборудования.
станко-часов фрезерного оборудования.
Так как общий фонд рабочего времени станков данного типа не может превышать 120, то должно выполняться неравенство

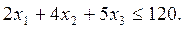
Аналогичные рассуждения относительно возможного использования токарного, сварочного и шлифовального оборудования приведут к следующим неравенствам:
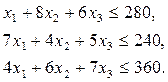
При этом, так как количество изготавливаемых изделий не может быть отрицательным, то
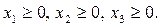 (1)
(1)
Далее, если будет изготовлено 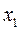 единиц изделий вида А,
единиц изделий вида А, 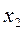 единиц изделий вида В и
единиц изделий вида В и 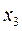 единиц изделий вида С, то прибыль от их реализации составит
единиц изделий вида С, то прибыль от их реализации составит 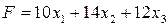 .
.
Таким образом, приходим к следующей математической задаче: дана система
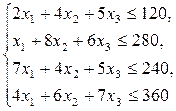 (2)
(2)
четыре линейных неравенства с тремя неизвестными 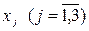 и линейная функция относительно этих же переменных
и линейная функция относительно этих же переменных
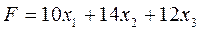 (3)
(3)
Требуется среди всех неотрицательных решений системы неравенств (2) найти такое, при котором функция (3) принимает максимальное значение. Как это сделать будет показано в дальнейшем.
Линейная функция (3), максимум которой требуется определить, вместе с системой неравенств (2) и условием неотрицательности переменных (1) образуют математическую модель исходной задачи.
Так функция (3) линейна, а система неравенств (2) содержит только линейные неравенства, то задача (1) – (3) является задачей линейного программирования.
 2015-03-22
2015-03-22 701
701








