Множественный регрессионный анализ

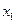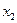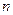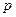В данном разделе эконометрики рассматриваются зависимости объясняемой переменной от двух и более объясняющих переменных , ,... Предполагается, что имеется наблюдений величины и величин 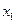, ,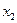... , 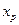между которыми имеется связь вида

.

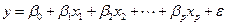Здесь 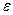случайная величина, распределенная по нормальному закону с нулевым средним и среднеквадратичным уклонением 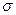. Будем считать, что коэффициент 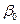стоит при переменной 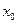, которая принимает все время одно и то же значение, равное 1. Тогда результаты наблюдений могут быть записаны в виде 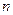–мерного вектор—столбца 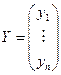и матрицы 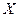размера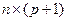

.

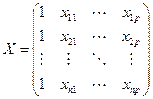В матрице 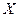каждый столбец представляет собой результаты наблюдений одной из величин 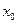, , 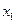,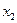... . 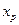В предположении независимости наблюдений, можно показать, что статистической оценкой параметров 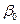, ,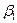…, , 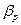имеющей наименьшую дисперсию, является 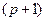-мерный вектор

.

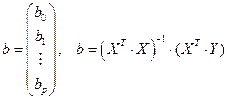Здесь и далее 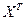– транспонированная матрица 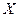. Уравнение линейной множественной регрессии имеет вид

.

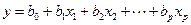Раздельное влияние на объясняющих переменных характеризуется стандартизированными коэффициентами регрессии 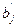и коэффициентами эластичности ().

,

,

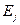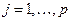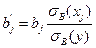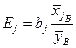где 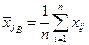, , 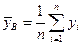, 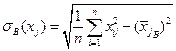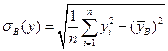. Стандартизированный коэффициент регрессии 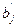является статистическим аналогом коэффициента корреляции зависимой переменной с 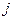–той объясняющей переменной 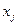. Коэффициент корреляции принимает значения из отрезка 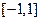. Равенство этого коэффициента 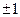указывает на функциональную зависимость между переменными , 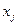. Наоборот, близость коэффициента корреляции к нулю позволяет сделать заключение о слабой зависимости между и 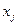. Коэффициент эластичности 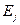показывает, на сколько процентов изменится в среднем значение величины при увеличении только одной переменной 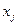на 1%.

Коэффициент детерминации регрессии 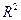определяется по формуле

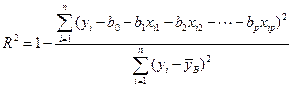
и показывает, какая доля в изменении зависимой переменной обусловлена влиянием переменных 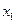, ,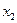... . 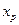Остаток 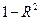, соответственно, показывает долю стохастической части 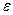в зависимости

.

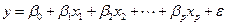Зная коэффициент детерминации 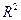, можно проверить гипотезу о значимости уравнения регрессии на заданном уровне значимости 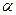. Гипотеза принимается, если выполнено неравенство

,

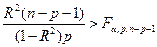где, как и раньше, 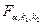¾ критическая точка распределения Фишера-Снедекора с вероятностью 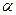и числом степеней свободы 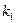и .

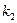Выпишем формулы доверительных интервалов для параметров уравнения линейной регрессии, а также доверительные интервалы для среднего и индивидуального значений переменной при заданных значениях , ,... .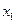

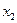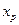Определим точечную оценку 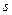параметра 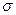случайной величины 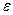в зависимости 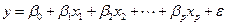по формуле

.

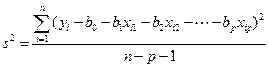Зададим доверительную вероятность 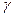. Доверительный интервал с доверительной вероятностью 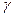для 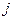–того коэффициента регрессии задается неравенством

, ,

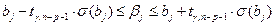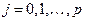где 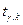- критическая точка распределения Стьюдента с вероятностью 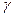и числом степеней свободы 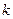, а

,

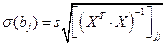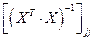( ¾ элемент, стоящий на диагонали матрицы 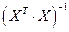на 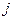–том месте).

Доверительный интервал с доверительной вероятностью 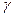для среднего значения переменной при заданных значениях переменных 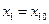, , 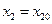…, 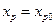определяется формулой

,

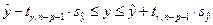где

,

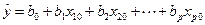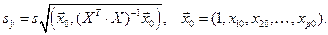
Здесь 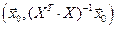¾ скалярное произведение векторов 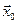и .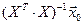

Для индивидуальных значений переменной соответствующий доверительный интервал несколько больше:

,

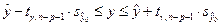где .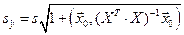

Задача 11.2. Имеются следующие данные о выработке литья на одного рабочего x ₁ (т), браке литья x ₂ (%) и себестоимости 1 т литья (т. руб.) по 10 литейным заводам:

I
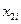yi

I
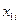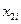yi

В предположениях классической линейной модели требуется:

1) найти множественный коэффициент детерминации и пояснить его смысл;

2) найти уравнение 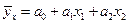множественной регрессии 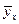на x ₁, x ₂, и оценить значимость этого уравнения и его коэффициентов на уровне a =0.05;

3) сравнить раздельное влияние на зависимую переменную каждой из объясняющих переменных, используя стандартизированные коэффициенты регрессии и коэффициенты эластичности;

4) найти 95 %-ные доверительные интервалы для коэффициентов регрессии, а также доверительные интервалы для среднего и индивидуального показателей значения себестоимости 1 т литья в цехах, в которых выработка литья на 1 рабочего составляет 17т, а брак литья - 7%.

Решение. По данным задачи выпишем вектор 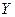и матрицу 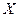, и определим коэффициенты уравнения линейной регрессии.

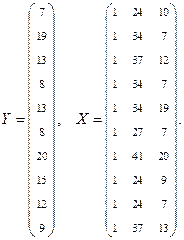
Тогда

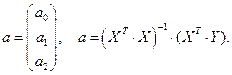
Найдем последовательно матрицу 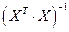и вектор 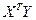. Имеем

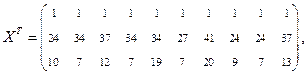
откуда

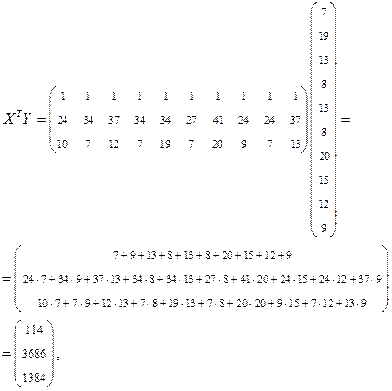
и, кроме того,

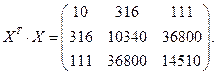
Теперь вычислим обратную матрицу :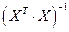

.

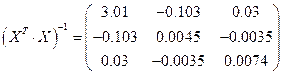Остается перемножить матрицу 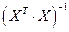и вектор :

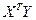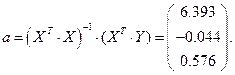
Таким образом, уравнение регрессии имеет вид:

.

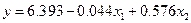Найдем точечные оценки для всех имеющихся переменных.

,

,

,

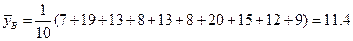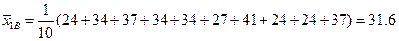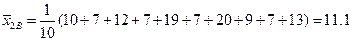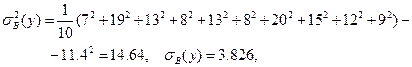
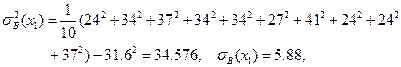
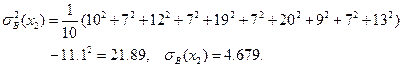
Теперь мы в состоянии определить коэффициент детерминации уравнения регрессии

.

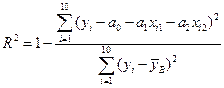Вычислим сначала сумму

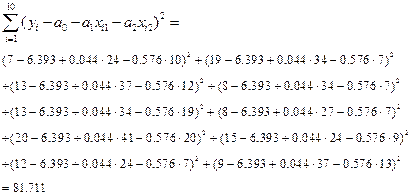Отметим, что

,

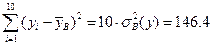откуда следует, что

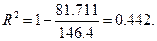
Коэффициент детерминации 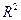интерпретируется как доля изменения зависимой переменной, обусловленная изменением независимых переменных, то есть в нашем случае изменение на 44.2% связано с изменением значений переменных 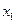и 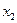и на 55.8% со случайными факторами.

Чтобы проверить гипотезу о значимости уравнения регрессии на уровне значимости 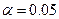, воспользуемся критерием значимости

.

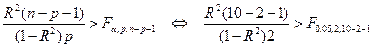В нашем случае

,

,

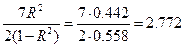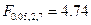и условие значимости не выполняется, что означает, что на выбранном уровне значимости гипотезы (когда мы хотим, чтобы вероятность ошибки первого рода была достаточно мала) экспериментальные данные позволяют считать, что на самом деле линейная часть уравнения регрессии равна нулю, и разброс значений переменной связан только со случайными факторами.

Найдем стандартизированные регрессии и коэффициенты эластичности для каждой из объясняющих переменных. Имеем:

,

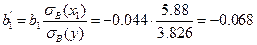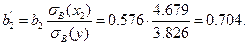
То, что выборочный коэффициент корреляции больше для переменной 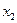указывает на то, что в нашем примере второй параметр более тесно связан с независимой переменной, чем первый. Далее,

,

,

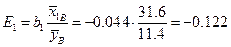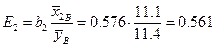откуда можно сделать вывод, что при увеличении величины 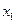на 1% величина уменьшается на 12.2%, в то время как увеличение 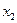на 1% дает прирост на 56.1%.

Найдем 95 %-ный доверительный интервал для коэффициентов регрессии. Нам потребуется точечная оценка параметра 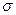стохастической части зависимости случайной величины от , :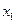

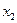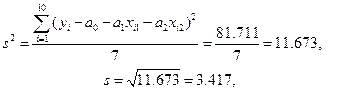
(сумма 81.711 в числителе этой формулы была найдена ранее при вычислении коэффициента детерминации ).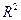

Доверительные интервалы с доверительной вероятностью 0.95 для коэффициентов регрессии имеют вид

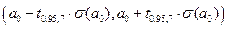для коэффициента ,

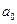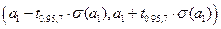для коэффициента ,

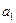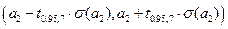для коэффициента ,

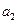где

,

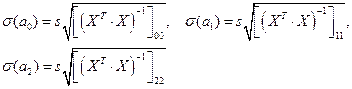элементы, стоящие на диагонали матрицы 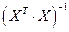. Матрица 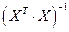была ранее найдена в явном виде, поэтому

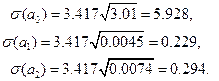
С учетом того, что 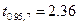получаем три доверительных интервала для коэффициентов соответственно:

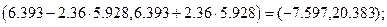
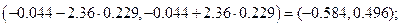
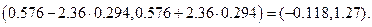
Определим теперь доверительные интервалы для среднего и индивидуального показателей значения себестоимости 1 т литья в цехах, в которых выработка литья на 1 рабочего составляет 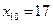т, а брак литья - 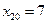%. Формула для доверительного интервала для средних значений переменной имеет вид

,

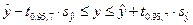где

,

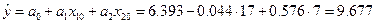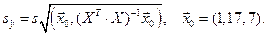
Получаем

,

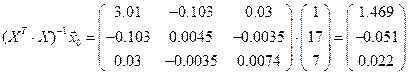
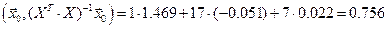откуда

.

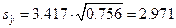Тем самым доверительный интервал определен:

.

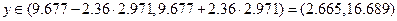Для индивидуальных значений переменной соответствующий доверительный интервал имеет вид:

,

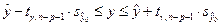где

,

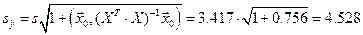откуда

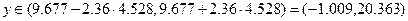
Элементы анализа временных рядов.

Частным случаем зависимости одной переменной от другой является так называемый временной ряд, когда независимая переменная есть время 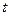, а зависимая переменная 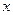есть значения некоторого числового параметра в моменты времени 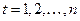. При статистическом исследовании зависимости 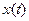можно применять стандартный регрессионный анализ и искать 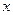как функцию от 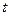: 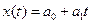. Очень часто, однако, более эффективно бывает использование статистических моделей, основанных на автокорреляции, то есть построении регрессий вида 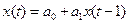или 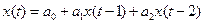. Изложим основные положения этой теории, необходимые для выполнения контрольной работы.

Пусть имеется ряд наблюдений переменной :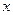

.

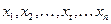Среднее значение временного ряда определяется по формуле

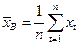
Выборочная дисперсия есть следующая сумма

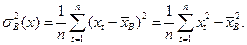
Уравнение линейной регрессии в предположениях нормальной классической модели (то есть в предположении, что 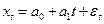, где 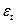¾ независимые нормально распределенные случайные величины с нулевым средним и одним и тем же средним квадратичным уклонением 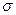) имеет вид

,

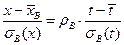где

,

,

.

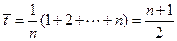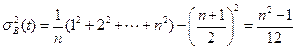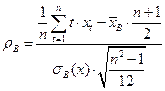Окончательно,

.

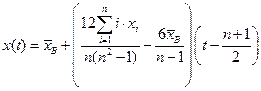Значимость регрессии на уровне 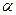проверяют так же, как в задаче 11.1. А именно, находят коэффициент детерминации

,

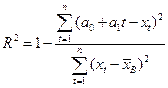а затем проверяют неравенство

,

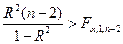где 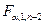есть критическая точка распределения Фишера-Снедекора (уравнение регрессии считают значимым, если неравенство выполнено).

Коэффициентом автокорреляции 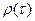с лагом 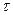называется коэффициент корреляции между рядом 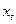и его сдвигом 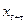на время 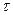(при этом оба ряда рассматриваются только в те моменты времени 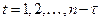, когда оба они определены):

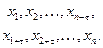
По определению выборочного коэффициента корреляции получаем:

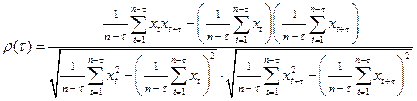В простейшем случае 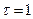получаем:

.

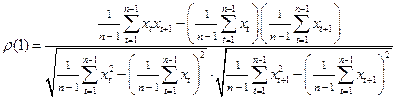Коэффициент автокорреляции показывает, насколько влияют реализации величины в предшествующие моменты времени на ее значение в будущем. При высокой автокорреляции стандартные регрессионные модели (то есть зависимости вида 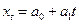) являются не вполне адекватными и следует использовать авторегрессионные модели.

Если в изучаемом временном ряду наряду с постоянно действующим фактором (трендом) имеется еще периодическая (сезонная) зависимость, или имеет место высокая степень автокорреляции, то для выявления тренда и устранения влияния случайных факторов производят так называемое сглаживание временного ряда методом скользящей средней с лагом 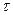( 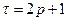произвольное нечетное число). Для этого ряд

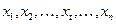
заменяют рядом

,

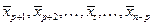где

.

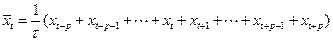Уравнение авторегрессии временного ряда 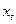с лагом 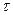есть линейное уравнение множественной регрессии зависимой величины 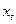на объясняющие величины 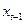, , 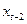…, 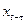вида

.

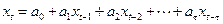Построение этого уравнение производится так же как в задаче 11.2, то есть по формуле

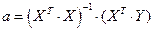
где

.

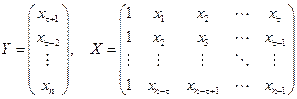Задача 11.3. Имеются следующие данные о поквартальном обороте торговой фирмы за 5 лет:

Номер квартала	Товарооборот (в % к предыдущему году)	Номер квартала	Товарооборот (в % к предыдущему году)

1) Постройте график временного ряда, приняв значение товарооборота на начальный момент времени равным 1.

2) Найдите среднее значение, среднее квадратичное отклонение и коэффициенты автокорреляции временного ряда.

3) Найти уравнение тренда временного ряда, полагая, что он линейный, и проверить его значимость на уровне a = 0.05.

4) Провести сглаживание временного ряда методом скользящих средних с интервалом сглаживания k =5.

5) Найти уравнение авторегрессии для временного ряда с лагом 2.

Решение. 1) Для графической интерпретации данного временного ряда используем программу MATHCAD. Для этого зададим вектор как матрицу и используем встроенную функцию PLOT.

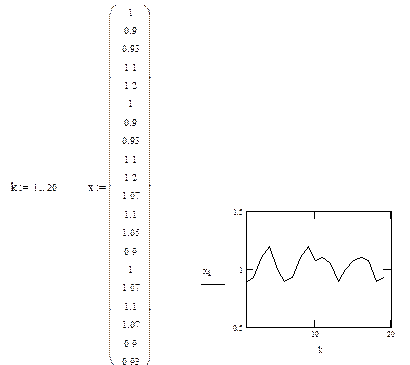
Среднее значение временного ряда находим с помощью следующих команд:

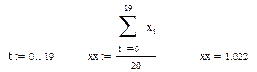
Таким образом, 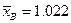. Среднее квадратичное уклонение также легко определить с помощью команд MATHCADа:

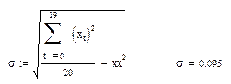
Следовательно, 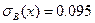. Подставим полученные данные в уравнение линейной регрессии:

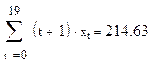
Отсюда

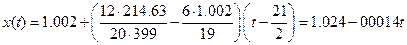
Проверим гипотезу о значимости уравнения регрессии на уровне значимости 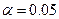. Вычислим коэффициент детерминации

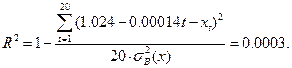
Как мы видим, коэффициент детерминации очень мал, что означает отсутствие какого-либо заметного влияния временнóго тренда на 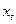(то есть изменения 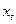случайны и не зависят от 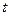). Действительно,

,

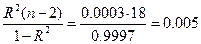в то время как

,

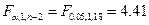и, следовательно, уравнение регрессии не значимо.

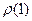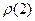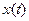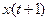Определим коэффициенты автокорреляции и . Коэффициент автокорреляции с лагом 1 – это коэффициент корреляции между случайными величинами и . Определим его по формуле

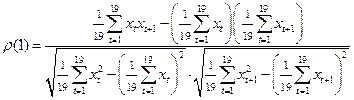
с помощью программы MATHCAD.

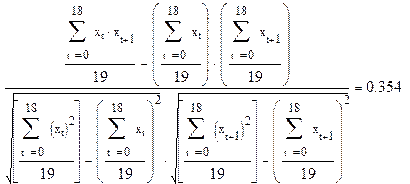
Таким образом, 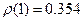, что свидетельствует о невысокой степени зависимости между 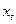и 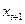. Аналогично рассчитывается коэффициент :

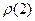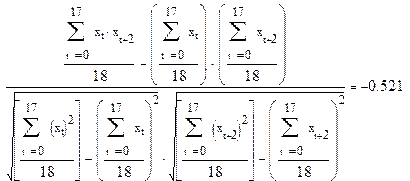
Таким образом, 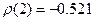, то есть связь между 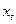и 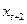возрастает.

Теперь проведем сглаживание временного ряда методом скользящих средних с лагом 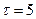. Усредненный временной ряд будет определен при 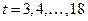и последовательно определяется по формулам:

,

,

,

,

,

,

,

,

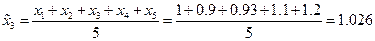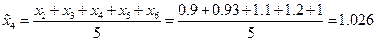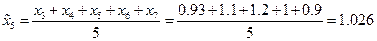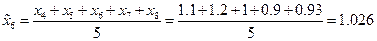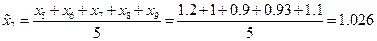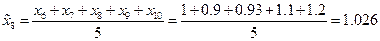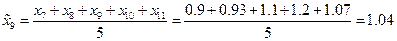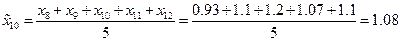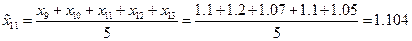
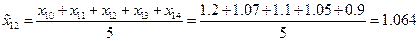
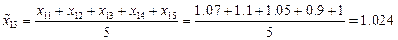
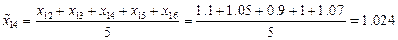
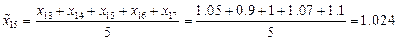
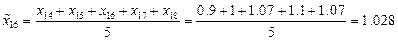
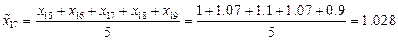
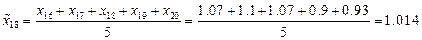Интересно построить график сглаженного ряда, чтобы наглядно продемонстрировать, что его поведение значительно менее стохастично, чем поведение исходного временного ряда.

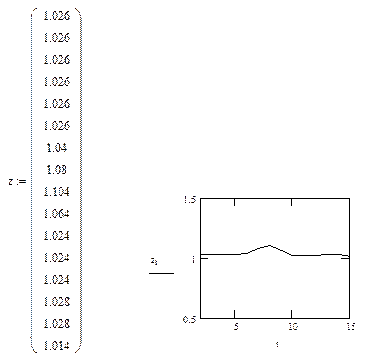
В заключение, найдем уравнение авторегрессии для временного ряда с лагом 2. Это уравнение представляет собой линейное уравнение регрессии зависимой величины 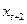от двух объясняющих величин 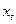и 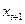, то есть

.

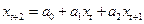Используем формулу

,

,

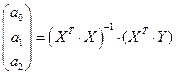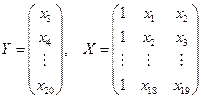и рассчитаем параметры этого вектора с помощью программы MATHCAD.

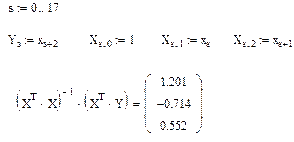
Итак, уравнение авторегрессии рассматриваемого ряда с лагом 2 имеет вид 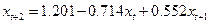. Посмотрим, насколько соответствует исходным данным уравнение линейной регрессии 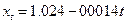и уравнение авторегрессии, для чего построим графики этих трех зависимостей.

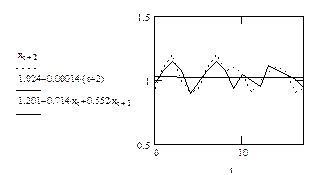
Как мы видим из рисунка, уравнение авторегрессии (в отличие от линейной регрессии) очень точно “накладывается” на график эмпирической зависимости и может служить для предсказаний поведения 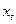в будущем.

Литература

1. Исследование операций в экономике (под ред. Н. Ш. Кремера). М.: ЮНИТИ, 1997.

2. Солодовников А.С., Бабайцев В.А., Бранков А.В. Математика в экономика. М.: Финансы и статистика, 1998.

3. Колемаев В.А., Математическая экономика. М.: ИНФРА-М, 1999.

4. Колемаев В.А., Математические методы принятия решения в экономике. М.: Финстатинформ, 1999 (учебник)

5. Х. Таха. Введение в исследование операций. Т.1,2. Москва, Мир. 1985.

6. Калихман И. Л. Сборник задач по математическому программированию. Москва, Высшая школа. 1975.

7. Экономико-математические методы и прикладные модели /Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999.

8. Малыхин В. И. Финансовая математика. М.: Юнити, 2000.

9. Бородич. Эконометрика. М.: Новое знание. 2001.

10. Практикум по эконометрике (под ред. И. И. Елисеевой). М.: Финансы и статистика. 2001.

11. Кремер Н.Ш., Путко Б. А. Эконометрика. М.: ЮНИТИ, 2002.

15. Айвазян С. А. Основы эконометрики. М.: ЮНИТИ, 2001.

16. В. Е. Гмурман Теория вероятностей и математическая статистика. М.: Высшая школа, 2001.

17. В. Е. Гмурман Руководство к решению задач по теории вероятностей и математической статистике М.: Высшая школа, 2001.