Задача эконометрики заключается в оценивании параметров генеральной совокупности и в установлении зависимости объясняемых переменных от одного или нескольких объясняющих переменных на основании данных эмпирических наблюдений. Напомним основные понятия математической статистики и эконометрики, необходимые для выполнения контрольной работы.
Парный регрессионный анализ.
Предположим, что две величины, 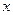 и
и  , связаны между собой стохастической зависимостью вида
, связаны между собой стохастической зависимостью вида
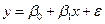 ,
,
где 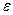 ¾ нормально распределенная случайная величина, с нулевым математическим ожиданием и средним квадратичным уклонением s, не зависящая от
¾ нормально распределенная случайная величина, с нулевым математическим ожиданием и средним квадратичным уклонением s, не зависящая от 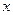 . Производится
. Производится 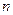 независимых наблюдений, в каждом из которых мы отслеживаем значения пары
независимых наблюдений, в каждом из которых мы отслеживаем значения пары 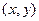 . Результатом такого статистического опыта является следующая выборка объема
. Результатом такого статистического опыта является следующая выборка объема 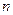 :
:
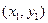 ,
, 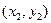 , …,
, …, 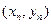 .
.
На основании этих данных мы пытаемся установить точечные и интервальные оценки параметров 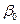 ,
, 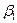 , а также точечные и интервальные оценки индивидуальных и средних значений переменной
, а также точечные и интервальные оценки индивидуальных и средних значений переменной  при различных уровнях фактора
при различных уровнях фактора 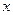 .
.
|
|
|
Теорема Гаусса—Маркова утверждает, что статистическими оценками параметров 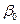 ,
, 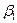 , имеющими наименьшую дисперсию в классе линейных несмещенных оценок, являются следующие величины. Оценкой
, имеющими наименьшую дисперсию в классе линейных несмещенных оценок, являются следующие величины. Оценкой 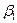 является величина
является величина
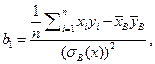
где
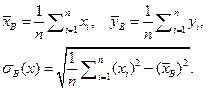
Для оценки параметра 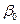 служит величина
служит величина
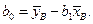
Теперь, если значение параметра 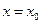 задано, то точечная оценка параметра
задано, то точечная оценка параметра  вычисляется по формуле
вычисляется по формуле
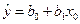 .
.
Интервальные оценки для 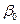 ,
, 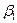 , а также оценки значений объясняемой переменной
, а также оценки значений объясняемой переменной  , основаны на следующей точечной оценке параметра
, основаны на следующей точечной оценке параметра 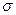 случайной величины
случайной величины 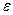 (стохастической части зависимости
(стохастической части зависимости 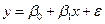 ):
):
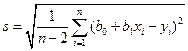 .
.
Доверительный интервал для параметра 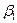 уравнения линейной регрессии с доверительной вероятностью
уравнения линейной регрессии с доверительной вероятностью 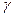 имеет вид:
имеет вид:
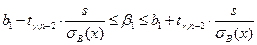 ,
,
где 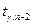 - критическая точка распределения Стьюдента с доверительной вероятностью
- критическая точка распределения Стьюдента с доверительной вероятностью 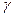 и числом степеней свободы
и числом степеней свободы 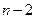 .
.
Доверительный интервал для оценки дисперсии 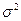 случайной величины
случайной величины 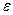 с доверительной вероятностью
с доверительной вероятностью 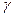 имеет вид:
имеет вид:
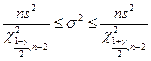 ,
,
где 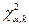 критическая точка распределения
критическая точка распределения 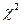 с доверительной вероятностью
с доверительной вероятностью 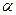 и числом степеней свободы
и числом степеней свободы 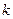 .
.
Доверительный интервал для средних значений объясняемой переменной  при выбранном уровне значений переменной
при выбранном уровне значений переменной 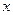 с доверительной вероятностью
с доверительной вероятностью 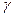 имеет вид
имеет вид
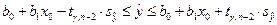 ,
,
где
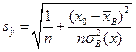 ,
,
а 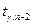 , по-прежнему, критическая точка распределения Стьюдента с доверительной вероятностью
, по-прежнему, критическая точка распределения Стьюдента с доверительной вероятностью 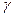 и числом степеней свободы
и числом степеней свободы 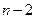 .
.
Доверительный интервал для индивидуальных значений объясняемой переменной  при выбранном уровне значений переменной
при выбранном уровне значений переменной 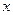 с доверительной вероятностью
с доверительной вероятностью 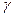 будет шире и определяется неравенством
будет шире и определяется неравенством
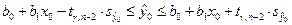 ,
,
где
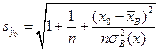 .
.
После определения параметров регрессионной модели следует проверить гипотезу о значимости линейного уравнения регрессии. Значимость уравнения регрессии означает, что линейная часть 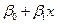 в зависимости
в зависимости 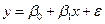 является существенной, отличной от нуля. Уравнение регрессии
является существенной, отличной от нуля. Уравнение регрессии 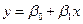 является незначимым, если разброс данных таков, что от выбора значений
является незначимым, если разброс данных таков, что от выбора значений 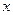 практически ничего не зависит, и изменения наблюдаемой величины
практически ничего не зависит, и изменения наблюдаемой величины  объясняется лишь наличием стохастической зависимости вида
объясняется лишь наличием стохастической зависимости вида 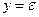 . Зададимся уровнем значимости гипотезы, равным
. Зададимся уровнем значимости гипотезы, равным 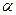 (уровень значимости гипотезы есть вероятность отвергнуть утверждение гипотезы в случае, когда оно на самом деле справедливо). Тогда гипотеза о значимости линейного уравнения регрессии принимается, если
(уровень значимости гипотезы есть вероятность отвергнуть утверждение гипотезы в случае, когда оно на самом деле справедливо). Тогда гипотеза о значимости линейного уравнения регрессии принимается, если
|
|
|
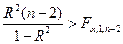 ,
,
где 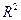 есть коэффициент детерминации, определяемый по формуле
есть коэффициент детерминации, определяемый по формуле
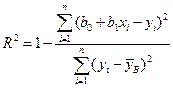 ,
,
а 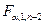 – критическая точка распределения Фишера-Снедекора с уровнем значимости
– критическая точка распределения Фишера-Снедекора с уровнем значимости 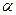 и числом степеней свободы 1 и
и числом степеней свободы 1 и 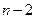 . В противном случае гипотезу о значимости регрессии на данном уровне значимости отвергают.
. В противном случае гипотезу о значимости регрессии на данном уровне значимости отвергают.
Если коэффициент детерминации 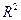 достаточно велик, и уравнение линейной регрессии можно считать значимым, то
достаточно велик, и уравнение линейной регрессии можно считать значимым, то 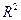 показывает, какая доля в изменении значений переменной
показывает, какая доля в изменении значений переменной  обязана изменению линейной части
обязана изменению линейной части 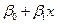 в соотношении
в соотношении 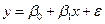 , в отличие от стохастической части
, в отличие от стохастической части 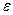 , которая обуславливает разброс значений
, которая обуславливает разброс значений  независимо от выбора
независимо от выбора 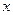 .
.
Квадратичная регрессия объясняемой переменной  на объясняющую переменную
на объясняющую переменную 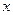 есть точечная оценка параметров стохастической зависимости
есть точечная оценка параметров стохастической зависимости
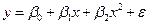 ,
,
где 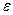 нормально распределенная случайная величина с нулевым математическим ожиданием и средним квадратичным уклонением
нормально распределенная случайная величина с нулевым математическим ожиданием и средним квадратичным уклонением 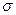 , не зависящая от выбора
, не зависящая от выбора 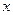 . Чтобы найти несмещенные точечные оценки
. Чтобы найти несмещенные точечные оценки 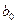 ,
, 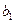 ,
, 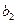 параметров
параметров 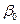 ,
, 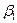 ,
, 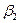 методом Гаусса, составим функцию
методом Гаусса, составим функцию
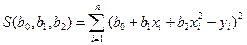 .
.
Искомые оценки есть решение задачи
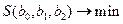 ,
,
которая по теореме Ферма сводится к решению следующей невырожденной системы линейных уравнений на неизвестные параметры 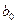 ,
, 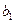 ,
, 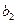 :
:

что может быть записано в виде
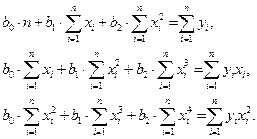
Вычислив коэффициенты при неизвестных в этой системе уравнений, мы любым известным способам (например, методом последовательных исключений переменных Гаусса) можем решить эту систему и определить значения коэффициентов квадратичной регрессии.
Задача 11.1. Имеются следующие данные о сменной добыче угля на одного рабочего y (т) и мощности пласта x (м) по 10 различным шахтам:
| i | |||||
| xi | |||||
| yi |
| i | |||||
| xi | |||||
| yi |
В предположении, что между условным среднем 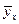 и x имеется связь вида
и x имеется связь вида 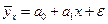 , где e - нормально распределенная случайная величина (не зависящая от x) с нулевым математическим ожиданием и среднем квадратичным уклонением s, определить:
, где e - нормально распределенная случайная величина (не зависящая от x) с нулевым математическим ожиданием и среднем квадратичным уклонением s, определить:
1) точечные оценки параметров a 0; a 1, s;
2) найти 95% доверительные интервалы для параметра a 1 уравнения регрессии и для параметра s;
3) среднюю добычу угля на одного рабочего для пласта мощностью 20 м;
4) найти 95% доверительные интервалы для средней и индивидуальной выработки рабочего для пласта мощностью 20 м;
5) проверить гипотезу о значимости уравнения регрессии на уровне значимости a =0.05;
6) определить коэффициент детерминации регрессионной модели.
Кроме того, методом наименьших квадратов Гаусса найти уравнение квадратичной регрессии 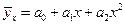 .
.
Решение. 1). Найдем сначала точечные оценки выборок для переменных 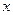 и
и  . Выборочные средние значения
. Выборочные средние значения 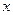 и
и  находим из соотношений
находим из соотношений
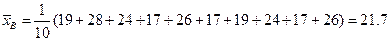 ,
,
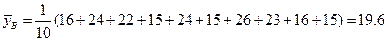 .
.
Для выборочных дисперсий и средних квадратичных уклонений получаем:
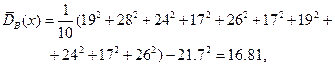
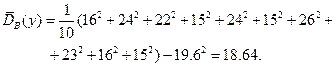
Отсюда
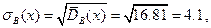
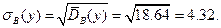
Для вычисления коэффициента линейной регрессии по формуле 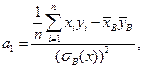 осталось найти смешанную сумму
осталось найти смешанную сумму
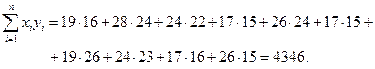
Отсюда следует, что
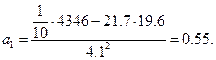
Из формулы 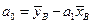 получаем оценку
получаем оценку 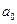
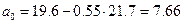 .
.
Таким образом, уравнение линейной регрессии имеет вид
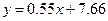 .
.
Теперь по формуле 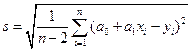 мы можем найти точечную оценку параметра
мы можем найти точечную оценку параметра 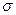 случайной величины
случайной величины 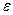 :
:
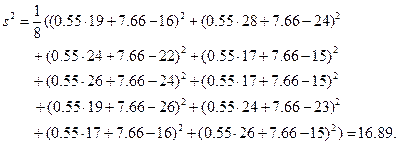
Отсюда 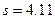 .
.
2) Найдем 95% доверительные интервалы для параметров 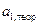 и s. Используем формулы
и s. Используем формулы
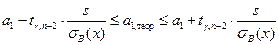 ,
,
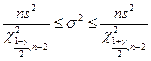 .
.
При 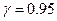 ,
, 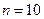 , критические точки распределения Стьюдента и распределения
, критические точки распределения Стьюдента и распределения 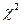 можно найти по таблицам этих распределений, и они равны соответственно
можно найти по таблицам этих распределений, и они равны соответственно
|
|
|
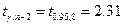 ,
,
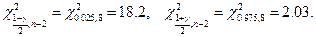
Отсюда следует, что доверительный интервал для параметра 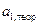 уравнения регрессии есть
уравнения регрессии есть
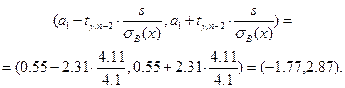
Аналогично, доверительный интервал для параметра 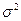 имеет вид
имеет вид
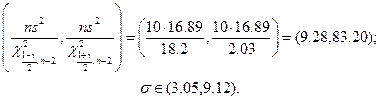
3) Найдем среднюю добычу угля на одного рабочего для пласта мощностью 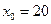 м. Подставим
м. Подставим 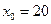 в уравнение линейной регрессии
в уравнение линейной регрессии 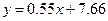 :
:
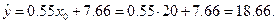
4) Найдем 95% доверительные интервалы для средней и индивидуальной выработки рабочего для пласта мощностью 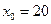 м. Используем формулы:
м. Используем формулы:
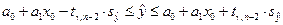 ,
,
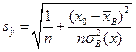 ,
,
для интервальной оценки средней выработки, и формулы
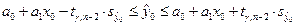 ,
,
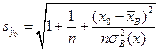
для интервальной оценки индивидуальной выработки. Получаем:
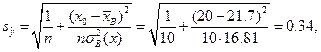
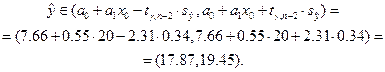
Аналогично, для интервальной оценки индивидуальной выработки получаем:
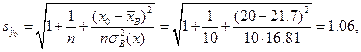
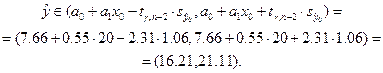
5) Проверим гипотезу о значимости уравнения регрессии на уровне значимости a =0.05. Для этого найдем коэффициент детерминации по формуле
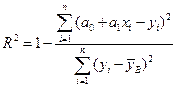 .
.
Получаем:
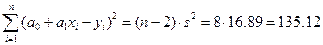 ,
,
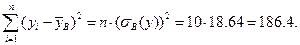
Следовательно,
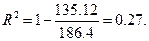
Критическая точка распределения Фишера-Снедекора при уровне значимости a =0.05 равна
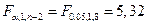 ,
,
откуда получаем, что
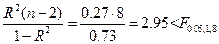 .
.
Следовательно, уравнение линейной регрессии следует признать незначимым на данном уровне значимости.
6) Коэффициент детерминации регрессионной модели был найден при проверке гипотезы о значимости уравнения регрессии. Поскольку 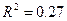 , следует заключить, что в зависимости объясняемой переменной
, следует заключить, что в зависимости объясняемой переменной  от
от 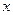 наиболее существенную роль играют случайные факторы, а не линейная часть регрессии
наиболее существенную роль играют случайные факторы, а не линейная часть регрессии 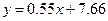 .
.
7) Найдем уравнение квадратичной регрессии 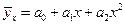 . Для этого подсчитаем коэффициенты линейной системы уравнений, которая определяется из принципа наименьших квадратов Гаусса:
. Для этого подсчитаем коэффициенты линейной системы уравнений, которая определяется из принципа наименьших квадратов Гаусса:
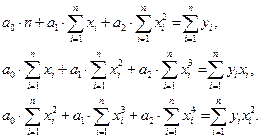
Часть коэффициентов этой системы фактически уже была найдена в предыдущих пунктах. А именно,
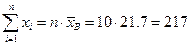 ,
,
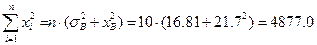 ,
,
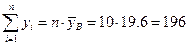 ,
,
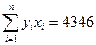 ,
,
Осталось, следовательно, вычислить три коэффициента системы.
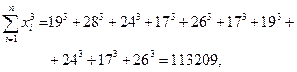
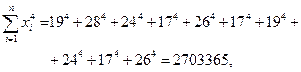
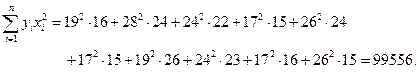 Получаем:
Получаем:
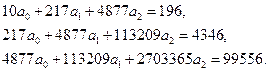
Для решения системы используем пакет символьных вычислений MATHCAD. Средствами этой программы решение системы линейных уравнений производится с помощью следующих командных строк.
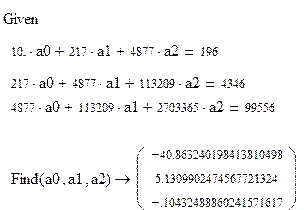
Решениями системы являются числа
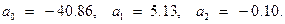
Таким образом, квадратичная регрессия имеет вид
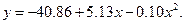
В заключение, построим графики функций 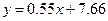 и
и 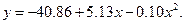 на отрезке
на отрезке 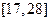 . Для построения графиков функций вновь используем программу MATHCAD.
. Для построения графиков функций вновь используем программу MATHCAD.
|
|
|
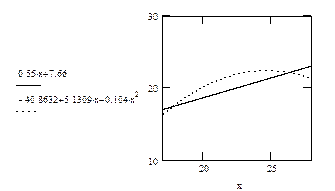
 2015-03-22
2015-03-22 1530
1530








