Обробка результатів вимірювань

Величини, що входять у формулу (6), є результатами вимірювань різних типів. Вимірювання d₁ і d₂ є результати прямих вимірювань. Вони обробляються стандартним способом, тобто розраховуються середньоарифметичні значення, випадкові похибки і систематичні похибки, рівна точності ноніуса штангенциркуля. Величини k і L – результати непрямих вимірювань. При розрахунку похибки величини 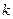можна вважати, що значення 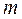і 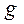відомі точно. Тоді формула для розрахунку похибки кожного окремого значення 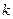матиме вигляд:

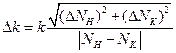. (7)

де 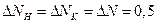мм – похибка відліку за дзеркальною шкалою, яка рівна половині ціни поділки шкали. Тоді формула (7) прийме вигляд .

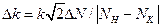Очевидно, що похибки 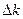будуть різними для різних величин k. Очевидно також, що максимальне значення похибки отримаємо в досліді з максимальною масою, оскільки значення |N_Н - N_К| у цьому випадку найменше. Саме цю похибку вважатимемо систематичною похибкою вимірювання 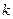, тобто 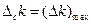. Тим самим вимірювання 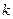штучно зроблені рівноточними. Далі розраховується середньоарифметичне значення 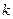і випадкову похибку за правилами обробки рівноточних вимірювань.

Вимірювання L також непряме. Враховуючи, що 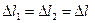, де 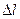– похибка показів мікрометра і рівна 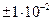мм, формула для розрахунку похибки окремого вимірювання приймає простий вигляд: 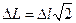. Ця похибка є систематичною похибкою визначення видовження, тобто 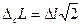. Середнє значення L і випадкова похибка його визначення розраховується звичайним способом.

Маючи інформацію про величини, що входять у формулу (6), і їх похибки, можна розрахувати середнє значення абсолютної похибки 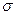, підставивши в (6) середні значення 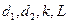. Тоді похибка 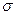обчислюється згідно формули:

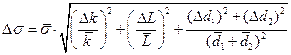(9)

Література

1.Лабораторный практикум по физике / Под ред. Ахматова А.С. – М.: Высшая школа, 1980.

2.Агапов Б.Т., Максютин Г.В., Островерхов П.И. Лабораторный практикум по физике. – М.: Высшая школа, 1982.

3.Евграфова Н.Н., Каган В.Л. Руководство к лабораторным работам по физике. – М.: Высшая школа, 1970.

4.Лабораторные занятия по физике / Под ред. Гольдина Л.Л. – М.: Наука, 1983.