Тема: решение уравнений с одной переменной в msexcel. Метод ложного положения

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

для обеспечения

управляемой самостоятельной работы студентов (УСР)

по учебной дисциплине

«Вычислительные методы и компьютерное моделирование»

Для специальности

Иностранный язык (английский).Информатика»

4-й курс

Всего УСР — 10 часов, 7 семестр

Лекция — 2 часа

Материалы подготовлены

Петлицкой Т.С.,

преподавателем кафедры физико-

математических дисциплин

(в соответствии с Положением об

управляемой самостоятельной работе

студентов БарГУ, утвержденным

30.08.2013 № 394)

Барановичи, 2014

ИНФОРМАЦИОННО-МЕТОДИЧЕСКАЯ ЧАСТЬ

ТЕМА: РЕШЕНИЕ УРАВНЕНИЙ С ОДНОЙ ПЕРЕМЕННОЙ В MS EXCEL. МЕТОД ЛОЖНОГО ПОЛОЖЕНИЯ.

Цель УСР:

– овладение учебным материалом дисциплины в объеме, требуемой учебной программой;

– формирование навыков самообразования в учебной, научной, производственной и управленческой деятельности;

– развитие учебных способностей, умений, навыков и принятия самостоятельных решений в профессиональной деятельности.

Вопросы для изучения:

1. Метод ложного положения MS Excel.

Цель работы:

изучить один из методов решения нелинейных уравнений – метод ложного положения.

Методические указания:

1. Изучить предлагаемый вопрос по литературным источникам.

2. Составить конспект.

3. Ответить на вопросы для самоконтроля.

Тема: РЕШЕНИЕ УРАВНЕНИЙ С ОДНОЙ ПЕРЕМЕННОЙ В MSEXCEL. МЕТОД ЛОЖНОГО ПОЛОЖЕНИЯ.

1. Метод ложного положения.

Рассмотрим еще одну модификацию метода Ньютона. Пусть известно, что простой корень 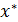уравнения 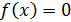находится на отрезке 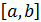и на одном из концов отрезка выполняется условие 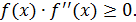Возьмем эту точку в качестве начального приближения. Пусть для определенности это будет 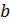. Положим 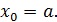Будем проводить из точки 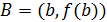прямые через расположенные на графике функции точки 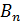с координатами 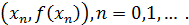Абсцисса точки пересечения такой прямой с осью 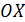есть очередное приближение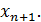

Геометрическая иллюстрация метода приведена на рисунке:

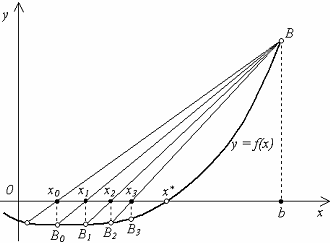
Прямые на этом рисунке заменяют касательные в методе Ньютона. Эта замена основана на приближенном равенстве:

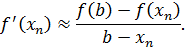
Заменим в расчетной формуле Ньютона производную 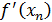правой частью приближенного предыдущего равенства. В результате получим расчетную формулу метода ложного положения:

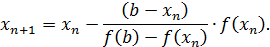
Метод ложного положения обладает только линейной сходимостью. Сходимость тем выше, чем меньше отрезок .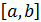

Критерий окончания. Критерий окончания итераций метода ложного положения такой же, как и для метода Ньютона. При заданной точности 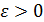вычисления нужно вести до тех пор, пока не будет выполнено неравенство:

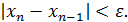
Пример: применим метод ложного положения для вычисления корня уравнения 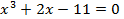c точностью 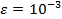на отрезке .

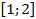Так как

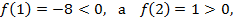
то на отрезке 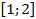есть корень.

Для ускорения сходимости возьмем более узкий отрезок 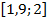, поскольку

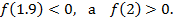
Вторая производная функции 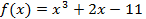равна .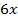

Условие 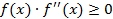выполняется для точки .

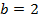В качестве начального приближения возьмем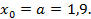

По расчётной формуле метода ложного положения имеем:

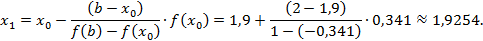
Продолжая итерационный процесс, получим результаты, приведенные ниже:

a	b	f(x)=x3+2x-11	f'(x)=3x2+2	f''(x)=6x	Выбор x0 и х1	e
		-8			x0=a, x1=b	0,001
xn-1	xn	f(xn-1)	f(xn)	f(b)	xn+1	ǀxn-xn-1ǀ<e
	1,9	-8	-0,341		1,925428784	-
1,9	1,925429	-0,341	-0,011046501		1,926243535	-
1,925429	1,926244	-0,011046501	-0,000351645		1,926269462	1,92624354

Ответ: корень уравнения 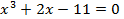равен 1,92624354.

Вопросы для самоконтроля

1. В чём суть метода ложного положения?

2. Почему этот метод называется «ложным»?

3. Критерий окончания метода ложного положения.

Список литературы

1. Численные методы: Учебно пособие для студентов вузов ∕ М. П. Лапчик, М. И. Рагулина, Е.К. Хеннер; под ред. М. П. Лапчика. — М.: Издательский центр «Академия», 2004.

2. Численные методы в примерах и задачах: Учебное пособие /В.И. Киреев, А.В. Пантелеев. — 3-е изд. стер. — М.: Высш. шк., 2008.

3. Вычислительная математика в примерах и задачах/ Н. В. Копченова, И. А. Марон. Главная редакция физико-математической литературы изд-ва «Наука», М., 1972.

Форма контроля: проверка конспекта.