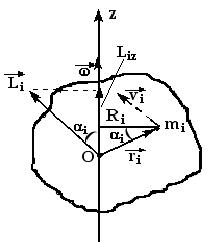
 Рис.1.18. Момент импульса тела относительно неподвижной оси Рис.1.18. Момент импульса тела относительно неподвижной оси | Рассмотрим i-ю точку твердого тела, вращающегося вокруг неподвижной оси Oz (рис.1.18). Если 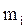 и и 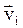 - масса и скорость точки, а - масса и скорость точки, а 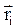 - ее радиус-вектор относительно т. О, то момент импульса - ее радиус-вектор относительно т. О, то момент импульса 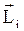 точки равен: точки равен: 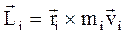 , а его модуль , а его модуль 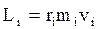 . Здесь учтено, что векторы . Здесь учтено, что векторы 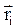 и и 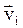 взаимно перпендикулярны взаимно перпендикулярны 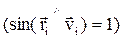 . Проекция момента импульса . Проекция момента импульса 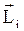 на ось Oz равна: на ось Oz равна: |
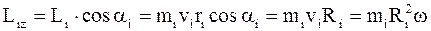 ,
,
где 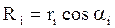 - радиус окружности, по которой движется i-я точка при вращении тела;
- радиус окружности, по которой движется i-я точка при вращении тела; 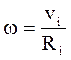 - угловая скорость вращения.
- угловая скорость вращения.
Момент импульса всего тела относительно оси Oz
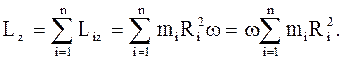 (1.46)
(1.46)
Произведение массы точки на квадрат ее кратчайшего расстояния до оси вращения называется моментом инерции точки относительно этой оси:
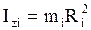 . (1.47)
. (1.47)
Величина
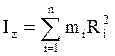 (1.48)
(1.48)
называется моментом инерции тела относительно этой оси.
С учетом (1.48) перепишем (1.46) в виде:
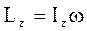 . (1.49)
. (1.49)
Подставим (1.49) в уравнение (1.45) вращательного движения тела относительно оси Oz:
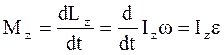 ,
,
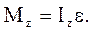 (1.50)
(1.50)
Это уравнение справедливо только в том случае, когда 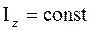 . Из сравнения (1.50) со вторым законом Ньютона
. Из сравнения (1.50) со вторым законом Ньютона 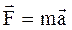 можно сделать вывод, что момент инерции
можно сделать вывод, что момент инерции 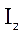 является мерой инерции твердого тела, вращающегося вокруг неподвижной оси, и учитывает не только массу, но и ее распределение относительно оси вращения.
является мерой инерции твердого тела, вращающегося вокруг неподвижной оси, и учитывает не только массу, но и ее распределение относительно оси вращения.
 2015-03-27
2015-03-27 2452
2452
