Концепция Блейка – Хэйнса

Зависимость угла смачивания от скорости.

Основные подходы и проблемы динамического смачивания.

Концепция Блейка – Хэйнса.

Как уже упоминалось, закрепленность, особое состояние периметра смачивания особенно сильно проявляется в динамике, т.е. при движении ТФГ.

Зависимость угла смачивания от скорости перемещения ТФГ была впервые замечена Аблеттом [26], который обнаружил, что при увеличении скорости угол натекания в системе парафин – вода возрастает до предельной скорости 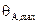, а краевой угол оттекания уменьшается до предельной величины 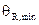, что достигается при одной и той же скорости ~0,44 мм/мин. При дальнейшем увеличении скорости углы смачивания оставались постоянными. Последующие экспериментальные исследования зависимости углов натекания и оттекания от скорости, проведенные на разных системах [27, 29, 30, 180] подтвердили закономерности, обнаруженные Аблеттом, и, кроме того, обнаружили существование области независимости угла смачивания от скорости не только при больших, но также при малых скоростях движения ТФГ.

Зависимость угла смачивания от скорости обсуждалась в целом ряде обзоров [181-188], в которых был сделан вывод, что причиной этой зависимости могут быть два эффекта:

1) гидродинамический эффект, т.е. более высокая скорость движения частиц жидкости в центральной части капилляра по сравнению ее со скоростью вблизи его стенок, что приводит к возрастанию 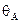и соответственно к уменьшению ;

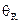2) эффекта замедленности установления равновесных величин поверхностных энергий трехфазной системы во время движения ТФГ.

Первый эффект, очевидно, значителен для случаев натекания и оттекания жидкости по предварительно смоченной поверхности (особенно при больших скоростях движения), а также при практически полном смачивании, и был объектом изучения относительно большего числа работ, чем второй. В случае движения жидкости по сухому, т.е. покрытому только адсорбционной пленкой жидкости твердому телу (при ограниченном смачивании) определяющим эффектом, по крайней мере при небольших скоростях движения, является, по-видимому, второй.

Теоретические работы по кинетике смачивания связаны, в основном, с рассмотрением гидродинамики течения жидких пленок и основаны на гидродинамической теории смазки. Основную трудность решения задачи растекания составляет описание зоны трехфазной границы, поскольку особенность течения жидкости при смачивании состоит в том, что при растекании в зоне ТФГ нарушается гидродинамическое условие прилипания. Рукенштейн и его школа делали попытки обойти эту трудность введением в задачу проскальзывания в зоне ТФГ [189-192]. Фриц [193]рассматривал движение мениска жидкости при натекании на смачивающую пленку (зоны ТФГ в полном смысле этого слова в данном случае нет). Решение этой задачи привело автора к оригинальной трактовке динамического угла смачивания, однако, как показали Калинин и Старов [194], некоторые выводы автора оказались ошибочными. Дальнейшее развитие эти представления нашли в работе [195], где в рассмотрение было введено расклинивающее давление. Более детальный анализ этих представлений с получением точных и приближенных решений был проведен Старовым с сотрудниками [194, 196]. Эти подходы относятся, строго говоря, только к случаю полного смачивания и хорошо описывают, например, растекание капель органических жидкостей по стеклу. Попытка применить полученные соотношения к случаю ограниченного смачивания не дает удовлетворительного результата.

Сложность проблемы стимулировала развитие иных подходов к решению этой задачи. Самсонов и Щербаков [197,198] сформулировали задачу о растекании как задачу термодинамики необратимых процессов в рамках теории Онзагера. На основе определенных предположений о форме выражений для импульса силы в изучаемой системе и введения диссипативных членов, описывающих поверхностную вязкость и сопротивление движению ТФГ, авторы строят выражения для производства энтропии в изучаемой системе. На основании этих выражений записываются линейные соотношения Онзагера, исходя из которых авторы получают выражение для скорости движения ТФГ. Как и следовало ожидать, полученная зависимость хорошо описывает эксперимент по натеканию вблизи состояния равновесия.

Существует также подход, где в качестве движущей силы растекания рассматривается разность свободных энергий образования поверхностей твердое тело – газ и сумма свободных энергий образования поверхностей твёрдое тело-жидкость, и жидкость – газ. Это направление разрабатывается Суммом [199-204] и Быховоким [205-208]. Получаемые соотношения хорошо описывают растекание жидких металлов по различным поверхностям, однако оценка правильности значений получаемых параметров затруднительна в силу практической невозможности определить свободную энергию образования твердой поверхности.

Если в гидродинамических подходах к проблеме динамики растекания зона ТФГ представляла осложняющий фактор, преодолеть который для случая конечного угла смачивания пока не удалось никому, то рассмотрение динамики растекания именно с точки зрения процессов, происходящих на линии трехфазной границы, оказалось чрезвычайно плодотворным. Действительно, если, как показывают многочисленные опыты и как уже упоминалось ранее, линия ТФГ является закрепленной, то именно процессы, происходящие на ней, должны определять общую динамику процесса, как наиболее медленные и наиболее энергоемкие. На необходимость учета "трения" периметра смачивания указывали многие авторы [27,30,128,136,137], однако наибольшего успеха в этом направлении добились Блейк и Хэйнс [209], которым удалось полностью описать теоретически экспериментальную кривую зависимости угла смачивания от скорости для скоростей, не превышающих ~10^-1 см/с. Они применили к процессу растекания подход Черри и Холмса [210], основанный на теории абсолютных скоростей химических реакций [211]. Согласно этому подходу, зона ТФГ фактически представляется как переходное состояние (активированный комплекс), через которое должна пройти система в ходе вытеснения одного флюида другим с поверхности твердого тела. Процесс вытеснения, согласно Блейку и Хэйнсу, проходит на активных центрах поверхности твердого тела, концентрация которых Δn является константой. Число замен молекулы из фазы I на молекулу из фазы 2 в единицу времени обозначается К₊ и, в соответствии с теорией абсолютных скоростей реакций реакций, равно [211]:

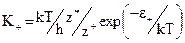
Где ε₊ – энергия активации процесса при абсолютном нуле, K₊ – скорость молекулярного переноса, k – постоянная Больцмана, h – постоянная Планка, T – температура, z^*, z⁺, z^- - суммы состояний для активированного, начального и конечного состояний.

Скорость обратного процесса равна

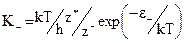
В состоянии равновесия суммарная скорость обмена равна 0, т.е.

К₊ = К_-

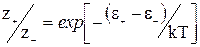
Дополнительные силы, необходимые для того, чтобы вызвать движение жидкости, не будут менять z⁺ или z^-, они могут рассматриваться как силы, изменяющие энергетические барьеры ε₊ и ε_-, понижая один и увеличивая другой. Работа, совершаемая этими дополнительными силами на единицу длины периметра смачивания описывается уравнением:

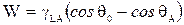, (Ш-62)

где W – работа сил смачивания. Если эта работа полностью затрачивается на увеличение или понижение ε₊ и ε_-, тогда

dw = W/Dn (Ш-63)

где Dn –концентрация активных центров на поверхности (число кинетических единиц процесса), δw - работа, совершаемая на каждом активном центре.

Суммарное вытеснение будет иметь положительное направление, т.к. будет уменьшать ε₊ и увеличивать ε_- на одну и ту же величину

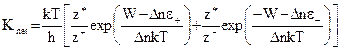
Так как К₊ = К_- = К, то можно записать, что

,

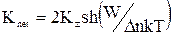и линейная скорость процесса определяется простым умножением

молекулярной скорости К_net на среднее расстояние между сорбционными центрами λ:

,

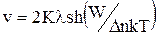v – линейная скорость переноса, l = (Dn)^-1/2 Ш-66)

Подставив значение W, авторы [209] окончательно получают:

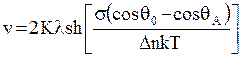
При малом аргументе гиперболического синуса, т.е. когда 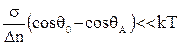уравнение (III-67) имеет вид

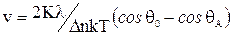(Ш-68)

При больших аргументах sh

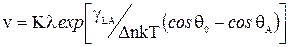
При обработке экспериментальных данных по вытеснению бензола водой в цилиндрическом капилляре по формуле (111-69), авторы получили значение Δn, согласующееся со значением концентрации силанольных групп на поверхности отекла.

Ш. 5.2. Исследование зависимости угла смачивания от скорости для воды в кварцевой щели и при капиллярном поднятии в стеклянных цилиндрических капиллярах.

Поскольку изучение зависимости угла смачивания от скорости имеет не только теоретическое (важное для понимания закономерностей смачивания), но и большое практическое значение (в различных природных и технологических процессах важно знать динамику смачивания), а данных по зависимости углов смачивания от скорости для воды и водных растворов на поверхности полярных твёрдых тел в литературе практически не было, нами были проведены соответствующие опыты [212,213].

Была изучена зависимость угла смачивания от скорости для воды в кварцевой плоскопараллельной щели, составленной из двух плоскопараллельных полированных пластин из природного кристаллического кварца размером 40x40 мм [212]. Ширина

щели составляла 400 мкм. Методика эксперимента описана в приложении.

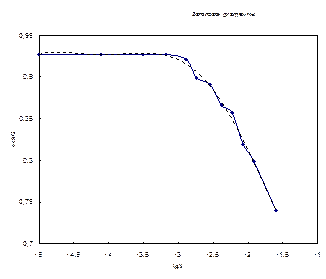Результаты опытов по радиальному растеканию воды в кварцевой щели позволили получить зависимость угла смачивания от скорости, которая приведена на рис.13.

Рис.13. Зависимость угла смачивания (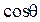)от скорости 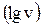, измеренная при растекании воды в плоскопараллельной кварцевой щели.

Как видно из рис.13, на зависимости 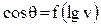хорошо видна область независимости θ от скорости, а также прямолинейная зависимость 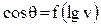для скоростей, больших 1,3·10^-3 см/с, что согласуется с уравнением (Ш-69) теории Блейка и Хэйнса.

Были также проведены опыты по капиллярному поднятию воды и водных растворов электролитов в цилиндрических стеклянных капиллярах из термометрического стекла (завод термометрического стекла в г.Клин) с радиусом просвета 52 и 54 мкм. Для исследования капиллярного поднятия нами использовались как свежетянутые капилляры (капилляры заводского изготовления, не бившие в контакте с водой после вытягивания), так и капилляры, подвергнутые стандартной процедуре очистки (см. методику в приложении). Как уже упоминалось, высокотемпературная обработка силикатов приводит к значительному дегидроксилированию поверхности [77]. Поэтому капилляры, полученные вытягиванием из расплава (~1000°) имеют дегидроксилированную поверхность. В контакте с парами воды гидроксильный покров восстанавливается частично. Полное восстановление гидроксильного покрова, по данным [77], происходит только при контакте с водой. Таким образом, поверхность свежетянутых капилляров, находящихся в равновесии с парами воды, является частично дегидроксилированной. Процедура очистки исходных капилляров, связанная с обработкой азотной кислотой и длительным промыванием водой, полностью восстанавливает 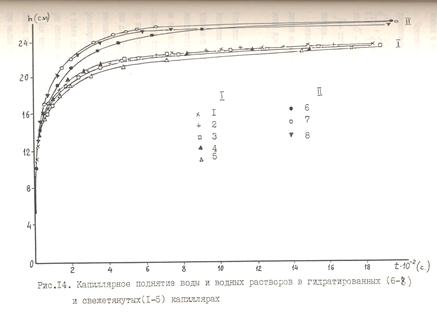гидроксильный покров поверхности. Поэтому капилляры, прошедшие процедуру очистки, будем в дальнейшем называть гидроксилированными. Кривые кинетики капиллярного поднятия в свежетянутых и гидратированных капиллярах, полученные для воды и различных растворов электролитов (кривые усреднены по 5-10 опытам) приведены на рис.14. В отличие от свежетянутых капилляров, где конечная высота капиллярного поднятия не устанавливалась в течение нескольких суток, в гидратированных капиллярах величина равновесного поднятия h_m устанавливалась через несколько часов после начала опыта и затем практически не изменялась. Кроме того, высота конечного поднятия в гидратированных капиллярах оказалась на 1–1,5 см больше, чем в свежетянутых.

Как известно, высота капиллярного поднятия h в цилиндрическом капилляре определяется уравнением

,

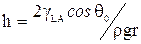где ρ – плотность воды, g – ускорение силы тяжести, r – радиус капилляра.

В соответствии с уравнением (Ш-70), различие высот поднятия в свежетянутых и гидратированных капиллярах может быть связано только с различием в величинах угла смачивания, поскольку все остальные величины, определяющие высоту поднятия в капилляре, одинаковы.

Аналогичная разница капиллярного поднятия для свежетянутых и гидратированных капилляров была обнаружена впоследствии в опытах на кварцевых капиллярах Березкиным и др. [214].

Наблюдаемое постепенное возрастание капиллярного поднятия в

свежетянутых капиллярах связано, по-видимому, с медленным

гидроксилированием их поверхности (образование в контакте с водой силанольных групп). Угол смачивания при этом уменьшается и высота поднятия растет. Кинетика капиллярного поднятия наиболее полно описывается уравнением Бриттина [216]:

,

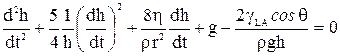где g– поверхностное натяжение жидкости, η – ее вязкость; ρ – плотность; g – ускорение силы тяжести; r – радиус капилляра.

Поскольку первые два члена этого уравнения по порядку величины намного меньше остальных, то ими для данного случая можно пренебречь, и тогда уравнение (Ш-71) упрощается

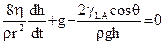(III-72)

Согласно этому уравнению, зная изменение скорости капиллярного поднятия 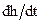можно проследить за изменением угла смачивания в процессе поднятия. Рассчитанные таким образом кривые зависимости cosθ от скорости капиллярного поднятия изображена на рис. 15 в координатах 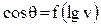. Скорости капиллярного поднятия 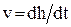определялись методом численного дифференцирования кривых 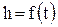. На рис. 15 приведен ряд кривых для гидратированных капилляров, характеризующих интервал изменений поднятия для изученной серии капилляров и разных растворов, кривая для поднятия воды в свежетянутых капиллярах, а также приведена для сравнения зависимость 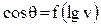для опытов по растеканию воды в кварцевой щели.

Как видно из рис.15, все представленные кривые для гидратированных поверхностей стекла и кварца имеют аналогичный вид: при малых скоростях (<10^-3см/с) угол смачивания практически не изменяется при увеличении скорости, в интервале скоростей 10^-3 –

10^-1 см/с наблюдается прямолинейная зависимость в координатах 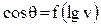и затем при скоростях > 10^-1 см/с, несмотря на большой разброс экспериментальных данных, можно, по-видимому, выделить вторую область независимости угла смачивания от скорости.

Полученные результаты качественно согласуются с результата­ми работ [26,30]. Зависимость 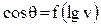, полученная на свежетянутых капиллярах, отличается от остальных отсутствием плато при малых скоростях поднятия, где наблюдается медленное постоянное уменьшение угла смачивания (возрастание ).

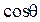Медленное уменьшение краевого угла, как уже указывалось, связано с регидроксилированием поверхности свежетянутых капилляров.

Интересно сопоставить полученные нами данные с результатами других авторов по зависимости углов смачивания от скорости движения ТФГ для воды и гидрофобных и гидрофобизированных поверхностях.

Из таблицы 1 видно, что величина максимального изменения 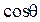при увеличении скорости (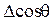) для гидрофильных поверхностей значительно выше, чем для гидрофобных, что связано, по-видимому, с сильным ориентирующим действием полярных твердых тел на молекулы воды. По-видимому, поэтому и максималь­ная скорость V_max после которой начинается вторая область независимости 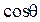от скорости, для гидрофильных тел также значительно выше.

По полученным зависимостям 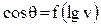можно определить константы теории Блейка и Хэйнса Δn и K, поскольку эти зависимости линейны в области скоростей 10^-3 – 10^-1 см/с. По тангенсу угла наклона экспериментальной прямой 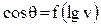и отрезку, отсекаемому ею на оси абсцисс, были определены величины Δn, K и λ, (в первом приближении l 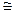(Dn)^-1/2). Для зависимости полученной для свежетянутых капилляров, расчет проводился по

Таблица I

Сравнение данных по зависимости угла смачивания от скорости, полученных разными авторами на различных системах

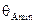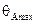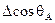
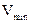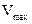Система	, град.	, град.		, см/с	, см/с	Ссылки
Кварцевая щель-вода		-	-	8 10-4	-	наши данные
Стекло – 10-3N КОН (гидратир. капилляр)			0,30	5·10-4	1·10 -1	то же
Стекло– 10-3 N HCl (гидратир.капилляр)			0,35	З·10-4	1,6 10-1	-
Стекло - вода (свежетянутый капилляр)			0,24	-	5·10-2	-
Стекло, покрытое (СH3)3SiCl – вода			0,17	8·10-4 – 4,2·10-3	5·10-3	[216]
Стекло, покрытое (СH3)2SiCl2 – вода			0,16	8.10-4. 4,2·10-3	1 10-2	[216]
Стекло, покрытое (C2H5)3SiCl– вода	78,5		0,03	8·10-4 – 4,2·10-3	1 10-2	[216]
Стекло, покрытое (C2H5)2SiCl2 – вода			0,06	8·10-4 – 4,2·10-3	1 10-2	[216]
Полиэтилен – вода			0,16	1,7·10-3	2,9·10-2	[30]
Парафин – вода			0,15	-	4 10-2	[26]
Политетрафторэтилен-вода			0,09	1 10-3	1,2 10-2	[217]

двум линейным участкам кривой 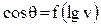, имеющим разный наклон, соответствующий медленному и быстрому падению 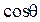с увеличением скорости. Рассчитанные таким образом константы уравнения Блейка-Хэйнса приведены в таблице 2.

Таблица 2

Константы уравнения Блейка-Хэйнса, вычисленные по экспериментальным данным

Система	cosθ0	Δn·10-18, м-2	Λ, нм	K·10-3, с-1
Стекло– 10-2N HCl (гидратир. капилляр)	0,976	1,7	0,8
Стекло – 10-2N КОН (гидратир. капилляр)	0,976	1,3	0,9
Кварц-вода (щель)	0,927	1,4	0,9
Стекло-вода (свежетяну-тый капилляр	Крутой наклон	0,881	1,01	1,0	7,9
Пологий наклон	0,881	0,44	1,5	0,25

Из таблицы 2 видно, что все вычисленные значения констант как для кварца, так и для гидратированного стекла хорошо сходятся между собой. Значения константы Δn, представляющей собой по Блейку и Хэйнсу концентрацию активных центров на поверхности стекла и кварца, оказались лежащими в пределах 1-2·10¹⁸ м^-2. Эти величины находятся в согласии с литературными данными, по которым величина поверхностной концентрации ОН-групп предельно гидроксилированной поверхности пористых стекол, силикагелей и аэросилов составляет 4,2-5,7·10¹⁸ м^-2. Тер-Минасян-Сарага [218] при исследовании адсорбции бромида додецилтриметиламмония на поверхности полированных пластин из стекла и плавленого кремнезема получила для концентрации поверхностных силанольных групп значения 1,9·10¹⁸ и 1,5·10¹⁸ м^-2 на стекле и кварце соответственно. Как видно из таблицы, величины Δn, полученные нами для отекла и кварца, хорошо согласуются с результатами этой работы. Сравнение значений Δn, рассчитанных по крутому и пологому участкам наклона кривой 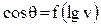для свежетянутых капилляров, показывает, что рассчитанная по крутому участку (большие скорости поднятия) величина Δn в 2-3 раза превышает величину Δn, рассчитанную по пологому участку (при малых скоростях поднятия). Последняя, по-видимому, и отражает слабую степень гидроксилирования поверхности свежетянутых капилляров. Как известно, регидроксилирование поверхности кремнеземов в воде связано со значительной энергией активации [77], причем повышение температуры позволяет ускорить этот процесс и полностью восстановить гидроксильный покров. По-видимому, при больших скоростях движения ТФГ выделение теплоты гидроксилирования и теплоты смачивания приводит к локальному повышению температуры зоны ТФГ, что способствует быстрому прохождению процесса регидроксилирования и понижению угла смачивания. Поэтому значение Δn, рассчитанное для больших скоростей поднятия в свежетянутых капиллярах практически совпадает со значением Δn для гидратированного стекла и кварца.

Вычисленные нами константы Δ n, K и λ были подставлены в полное уравнение Блейка-Хэйнса (III-67) [209]. Рассчитанные по этому уравнению теоретические кривые зависимости соs θ = f(lg v) приведены в виде сплошных линий на рис. 15. Из сравнения теоретических кривых с экспериментальными точками видно, что для всех рассмотренных случаев наблюдается хорошее совпадение эксперимента и теории, расхождение наблюдается лишь в области больших скоростей, где, по-видимому, для описания процесса растекания недостаточно рассмотрения только молекулярного переноса в зоне ТФГ и, по-видимому, нужно привлекать гидродинамическое рассмотрение растекания исследуемой системы.

Совпадение вида зависимостей соs θ = f(lg v),полученной в прямом эксперимента по смачиванию (кварцевая щель) и рассчитанной по капиллярному поднятию, говорит о том, что с учетом кинетики изменения угла смачивания при изменении скорости уравнение Бриттина правильно описывает процесс капиллярного поднятия для изученных систем. Нет нужды также подчеркивать, что угол смачивания не является постоянным при капиллярном поднятии и зависимость соs θ = f(lg v) необходимо включать в уравнение процесса капиллярного движения жидкости. К сожалению, эта зависимость до сих пор часто не учитывается при рассмотрении капиллярного поднятия жидкостей [198].