при различном состоянии адсорбционной пленки воды

На гидратированных капиллярах была проведено три серии опытов по температурной зависимости капиллярного поднятия с различной предварительной подготовкой поверхности. Как уже упоминалось, смачивающие пленки воды и водных растворов электролитов на поверхности стекла и кварца являются неустойчивыми и самопроизвольно распадаются на участки адсорбционной пленки и жидкости на поверхности. Было замечено, что если оттекание воды из полностью заполненного канала капилляра производить достаточно медленно, то за отступающим мениском остается адсорбционная плёнка, а капель и перетяжек жидкости не образуется. Критерием отсутствия последних в канале капилляра служило последующее плавное и полное (соответствующее расчету) капиллярное поднятие воды в капилляре. С капиллярами, адсорбционная пленка воды на поверхности канала которых образовалась описанным способом, было проведено 2 серии опытов. В первой серии капилляры со сформированной адсорбционной пленкой помещались в термостат, выдерживались там 15 минут, после чего проводились измерения зависимости h=f(t). В этом случае, по-видимому, пленка на поверхности не успевала достичь равновесия при данной температуре. Во второй серии капилляры с адсорбционной пленкой выдерживались в термостате перед опытом течение трех часов.

Третья серия опытов была проведена с капиллярами, которые после регидроксилирования поверхности протягиванием через канал бидистиллированной воды проходили процедуру медленного оттягивания воды (так, чтобы не образовались капли и перетяжки воды в канале), сушки в стеклянной ампуле при температуре 200°C и вакуумировании форвакуумным насосом в течение 6 часов. После остывания ампул в нее впускался воздух, очищенный увлажненный пропусканием через активированный уголь и дистиллированную воду. После этого капилляры помещались в термостат, где выдерживались над насыщенными парами воды при данной температуре в течение 2-6 часов в зависимости от температуры (для 20 и 30°C – 6 часов, для 40 и 50°C – 4 часа, для 60-70°C – 2 часа).

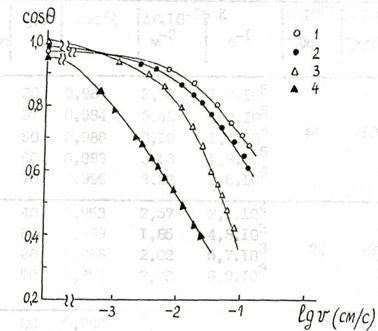
Рис.20. Зависимости соsq = f(lgv) для гидроксилированных капилляров с адсорбционной пленкой, сформированной: адсорбцией из воздуха (I - Р/Р₅ = 0,57; 2 - Р/Р₅= I) и в результате разрыва смачивающей пленки (3 - Р/Р₅ ~1, время выдерживания перед экспериментом 15 минут; 4 - Р/Р₅^1; время выдерживания 3 часа.).

В остальном методика исследования и расчета была такой же, как для свежетянутых капилляров. Проведенные опыты показали, что для гидратированных капилляров температурная зависимость кинетики смачивания выражена гораздо слабее, чем для свежетянутых. Во всех трех сериях скорость капиллярного поднятия воды с увеличением температуры, в общем, росла, но значительно меньше, чем для свежетянутых. Сравнение кинетики поднятия при одной и той же температуре для различных серий опытов показало, что наибольшая скорость поднятия наблюдалась для третьей серии опытов. На рис. 20 приведены зависимости cosq = f(lg v), рассчитанные по полученным кривым капиллярного поднятия для невысоких температур (20-40°C). На рис. 20 приведена также зависимость cosq – lg v, полученная ранее для капилляров при влажности воздуха Р/Р_s 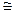0,55 (рис. 15). Хорошо видно сильное различие полученных зависимостей. Чем меньше значение cosq при данной скорости движения мениска, тем, очевидно, меньше высота поднятия при данной скорости. При этом величина

статического угла смачивания (и соответственно равновесная высота капиллярного поднятия) для всех проведенных при 20°C опытов остается практически постоянной. Сильные изменения претерпевает кинетика капиллярного поднятия, т.е. кинетика достижения равновесного угла смачивания. Результаты расчета параметров уравнения Блейка-Хэйнса для проведенных опытов приведены в таблице 4.

Таблица 4.

Константы уравнения Блейка-Хэйнса из данных по кинетике капиллярного поднятия для гидратированных капилляров

Серия опытов	Время приведения в равновесие (часы)	t, °C	cosθ0	Δ n ·10-18, м-2	К, с-1	Δ H ·1021, Дж	Δ S ·1023, Дж/К
	0,25		0,981	3,83	1,3·105		-10
	0,984	3,48	1,2·105
	0,988	3,19	1,4·105
	0,993	3,13	1,9·105
	0,996	3,22	2,6·105
			0,953	2,57	2,1·104		-22
	0,939	1,85	4,8·103
	0,966	2,02	5,7·103
	0,974	2,00	6,9·103
	2÷6		0,982	2,1	8,8·104	7÷15	–20÷–23
	0,964	1,9	9,2·104
	0,953	2,1	9,9·104
	0,897	1,9	7,8·104
	0,947	1,6	9,7·104
	0,937	1,8	15,1·104

1 и 2 серии - адсорбционная пленка после прорыва смачивающей;

3 серия - адсорбционная пленка из паров при Р/Р₃ ≈1.

Как видно из таблицы 4, изменение способа формирования адсорбционной пленки на поверхности капилляров заметно сказалось на всех параметрах уравнения Блейка-Хэйнса. Наибольшее значение Δ n и наибольшая величина K (параметра, характеризующего скорость смачивания) обнаруживаются в опытах первой серии, когда адсорбционная пленка формировалась путем разрыва смачивающей и выдерживалась при температуре опыта 15 минут, т.е., очевидно, не была равновесной. Для этого же случая наблюдается наименьшее по модулю значение энтропии

активации смачивания. Это может быть связано с тем, что образованная путем разрыва смачивающей плёнки адсорбционная плёнка не успевает достичь равновесной структуры и в значительной степени сохраняет характерное для смачивающей плёнки менее упорядоченное, менее структурированное состояние. Для этой же серии опытов характерна большая величина энтальпии активации смачивания, что может быть связано с тем, что образовавшаяся при разрыве смачивающей плёнки при 20° толстая, рыхлая адсорбционная плёнка не успевает достичь за 15 минут равновесного состояния и для удаления ее с поверхности при смачивании необходима значительная энтальпия активации.

Сравнение полученных данных между собой и с результатами опыта и расчёта для свежетянутых капилляров (таблица 3) показывает, что уменьшение значения Δ Η сопровождается увеличением Δ S по абсолютной величине и наоборот, т.е. в целом свободная энергия активации смачивания изменяется довольно незначительно. Тем не менее данные таблиц 3 и 4 позволяют заметить, что уменьшение статического угла смачивания (увеличение соsθ) сопровождается уменьшением величины свободной энергии активации смачивания.

Как уже упоминалось, в литературе имеются данные [127], что равновесный угол смачивания воды на кварце не зависит от температуры. Данных о зависимости углов смачивания на кварце от влажности воздуха, т.е. от толщины адсорбционной пленки в литературе отсутствовали. Нами была сделана попытка выяснения этого вопроса. Опыты по определению углов смачивания проводились на плавленом кварце марки КСГ для раствора HCl при рН=2 (т.е. в ИЭТ кварца) при влажности воздуха от 10 до 98 %, создаваемой насыщенными растворами соответствующих солей ZnCl₂, LiCl, Ca(NO₃)₂, NaCl, Na₂SO₄ и CuSO₄). Опыты показали, что величина угла смачивания очень мало изменяется с изменением влажности воздуха и колеблется в пределах 31-33°. Для опытов второй и третьей серии прежде всего характерны практически одинаковые значения Δn и ΔS при сильно отличающихся значениях К (скорость смачивания в третьей серии была значительно большей). К сожалению, довольно большой разброс экспериментальных данных для опытов третьей серии позволил определить только интервал изменения значений Δ Н (7÷15·1О^-21 Дж/центр), однако тем не менее эти данные показывают, что энтальпия активации смачивания в этом случае минимальная.

Проведенные опыты убедительно доказывают, что образование равновесной адсорбционной пленки воды на поверхности стекла процесс достаточно длительный.

Возвращаясь к уравнению (Ш-66) Блейка и Хэйнса и учитывая, что скорость молекулярного переноса К зависит как от исходного, так и от конечного энергетического состояния молекул, участвующих в переносе (смачивании), можно сделать вывод, что проведенные опыты по влиянию состояния адсорбционной пленки воды на кинетику смачивания находятся в согласии с общим представлением смачивания как процесса, который может быть описан с позиций теории абсолютных скоростей реакций [211].

Тот факт, что величина Δn, входящая в уравнение Блейка и Хэйнса, не является постоянной для одной и той же поверхности твердого тела свидетельствует, по-видимому, о том, что этот параметр не может быть отождествлен с концентрацией активных центров поверхности твердого тела, как предполагалось в [209], но представляет собой концентрацию кинетических единиц, участвующих в процессе смачивания. Очевидно, что эта величина связана с содержанием активных центров поверхности (концентрацией силанольных групп), поскольку имеет тот же порядок, но зависит также от состояния адсорбционной пленки. Необходимо отметить однако, что замеченная вариация величины Δn относительно невелика (изменение в 1,5- 2 раза).

Описанные выше опыты проводились в условиях, когда изменялось только состояние гранили твёрдое тело – пар, состояние границы твердое тело – жидкость оставалось неизменным. Представляло интерес проведение опытов по оценке влияния на кинетику смачивания изменения состояния границы твердое тело –жидкость при постоянстве состояния границы твёрдое тело – газ. Такое изменение осуществлялось вариацией состава раствора.

Ш.5.5. Влияние рН раствора на зависимость угла смачивания от скорости.

Очевидно, что наличие растворенных веществ, изменяющих состояние границы твердое тело – жидкость, должно влиять как на величину равновесного угла смачивания, так и на кинетику смачивания. О зависимости статических углов смачивания от состава и концентрации раствора электролитов речь пойдет в разделе III.7, здесь же остановимся на опытах по зависимости cosθ = f(lgv) для растворов с различным рН.

Опыты проводились в плоскопараллельной щели, составленной из полированных пластин плавленого кварца марки КСГ. Методика исследования аналогична методике для щели из пластин кристаллического кварца. Исследовалось растекание водных растворов НСl - КС1- КОH при постоянной ионной силе, соответствующей 10^-2н. при рН от 2 до 12 и скоростях движения ТФГ от 10^-4 до 10^-1 см/с. Проведенные опыты показали сильное влияние состава (рH) раствора на зависимость cosθ = f(lgv) (рис.21). Как видно из рис.21, с увеличением рН выше ТНЗ кварца (рН 2) наблюдается уменьшение cosθ (подробное обсуждение этой зависимости в разделе Ш.7), некоторое изменение наклона прямолинейного участка зависимости cosθ = f(lgv) при скоростях 10^-3- 10^-1 см/с, а также заметное смещение начала этого участка в сторону меньших скоростей. При увеличении рН выше ТНЗ область независимости угла смачивания от скорости ограничивалась меньшими скоростями движения ТФГ. Если для рН2 cosθ начинает уменьшаться при скоростях порядка 4·10^-3см/с, то для pH 12, уменьшение cosθ (увеличение θ) начинается уже при скоростях 5·10^-4 см/с, т.е. область зависимости cosθ от lgv смещается по оси скоростей на порядок.

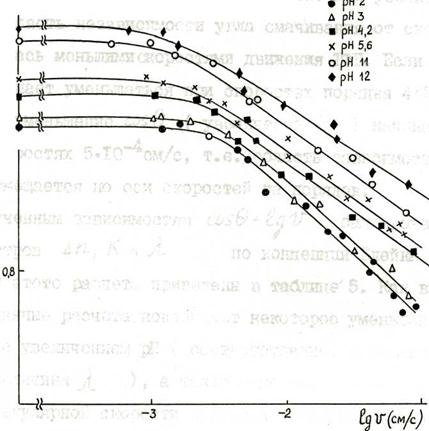
Рис.21. Зависимости cosθ = f(lgv) для растворов НС1 - КС1 - КОН при различных рН на плавленом кварце♦

По полученным зависимостям cosθ = f(lgv) был проведен расчет параметров Δn, K и λ по концепции Блейка и Хэйнса. Результаты этого расчета приведены в таблице 5. Как видно из таблицы, данные расчета показывают некоторое уменьшение величины Δn с увеличением рН (соответственно, несколько увеличитается величина λ), а также заметное уменьшение величины К (молекулярной скорости процесса). Сравнение значений Δn и К, полученных в этих опытах с данными для кристаллического кварца (щель) и стекла (стеклянные капилляры) для воды (таблица 2) показывает, что среднее значение Δn для плавленого кварца в ~1,5 раза меньше, чем для кристаллического кварца и стекла, что может быть связано со спецификой поверхности. Величина, К для раствора о pH 2 имеет тот же порядок, что и в предыдущих опытах, но сильно уменьшается с увеличением рН раствора.

Проведенные опыты убедительно доказывают, что изменение состояния границы твёрдое тело – жидкость, обусловленное изменением состава раствора так же, как и изменение состояния границы твёрдое тело – газ сильно сказывается на зависимости cosθ = f(lgv), хотя общий вид зависимости (наличие плато при малых скоростях движения и линейная зависимость cosθ = f(lgv) увеличении скорости) сохраняется для всех исследованных растворов.

Таблица 5.

Константы уравнения Блейка-Хэйнса для процесса растекания растворов НСl-КСl - КОН (10^-2 н.) с различными pH в щели из плавленого кварца марки КСГ.

pH	соs θ0	Vmin*103, см/с	Δn*10-13, см-2	λ, нм	К, с-1
	0,910	3,5	8,7	1,1	2,2*104
	0,920	3,0	7,9	1,1	2,0*104
4,2	0,934	2,0	6,9	1,2	1,6*104
5,6	0,946	1,8	6,7	1,2	1,1*104
	0,973	1,3	6,2	1,3	5,9*103
	0,980	1,2	6,2	1,3	5,0*103

V_min – минимальная скорость, при которой начинается уменьшение соs θ

Нужно отметить, что концепция динамического смачивания Блейка и Хэйнса рассматривает только сам молекулярный процесс смачивания и не учитывает возможные сопутствующие процессы. Это может быть перенос по газовой фазе, процесс течения по плёнке при условии её неравновесности, наконец, гидродинамические процессы в объемной жидкой фазе, особенно при достаточно малых краевых углах. Очевидно, что для полного описания процесса динамического смачивания необходим учёт всех этих явлений. Тем не менее, весь комплекс исследований, проведенных по динамическому смачиванию, позволяет сделать вывод, что применение теории абсолютных скоростей реакций дает очень хорошие результаты и в случае описания кинетики смачивания.

Опыты по растеканию растворов проводились таким образом, что адсорбционная плёнка воды на поверхности кварца не содержала растворенных веществ, поскольку формировалась из газовой фазы. Наличие в объемной фазе жидкости растворенных веществ должно приводить не только к изменению состояния границы твёрдое тело – жидкость, но и к диффузии растворенных веществ из фазы объемной жидкости в адсорбционную плёнку. Если коэффициент диффузии компонентов раствора в адсорбционной плёнке достаточно велик, то контакт её с водной фазой, содержащей электролит, может приводить к изменению величины σ_SA. Поскольку данные о величинах коэффициента диффузии электролитов в адсорбционных плёнках немногочисленны и противоречивы, нами были прове­дены соответствующие опыты.