Получение множества Ф1 (объединение формул 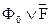 ) эквивалентно КНФ соответствующей формулы. Так как какая-либо интерпретация удовлетворяет формуле вида
) эквивалентно КНФ соответствующей формулы. Так как какая-либо интерпретация удовлетворяет формуле вида 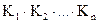 в том и только в том случае, если она удовлетворяет формулам и К1, К2, …, Кn одновременно, то исходную формулу Ф1 можно заменить множеством конъюнктивных членов (дизъюнктов).
в том и только в том случае, если она удовлетворяет формулам и К1, К2, …, Кn одновременно, то исходную формулу Ф1 можно заменить множеством конъюнктивных членов (дизъюнктов).
Пример. 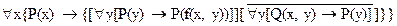 .
.
Исключим знаки импликации:
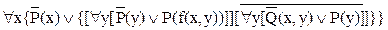 .
.
Уменьшим области действия знаков отрицания до одного предиката:
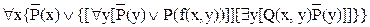 .
.
Произведем стандартизацию переменных:
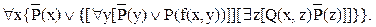
Проведем сколемизацию:
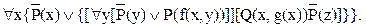
Здесь g(z) – функция Сколема, зависящая только от x, она находится в области действия квантора.
Получим предваренную форму формулы:
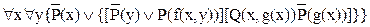 .
.
Исключим кванторы общности:
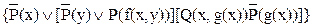 .
.
Используя закон дистрибутивности, получим КНФ:
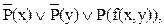
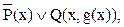
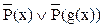 .
.
 2015-03-27
2015-03-27 442
442







