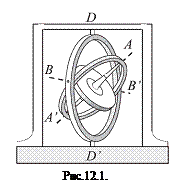
Теоретическая часть. Гироскопом называется массивное твердое тело (обычно диск), быстро вращающееся вокруг оси симметрии

Гироскопом называется массивное твердое тело (обычно диск), быстро вращающееся вокруг оси симметрии. Для того чтобы ось гироскопа могла принимать любое направление в пространстве, используется карданов подвес (рис.12.1). Гироскоп – диск, вращающийся вокруг оси AA'. Внутреннее кольцо может вращаться вокруг горизонтальной оси ВВ', перпендикулярной оси AA'. Внешнее кольцо может вращаться вокруг вертикальной оси DD'. Таким образом, у гироскопа есть три степени свободы. Точка пересечения всех трех осей AA', ВВ' и DD' совпадает с центром масс гироскопа, неподвижным относительно подвески. Такой гироскоп называется свободным.

При своем вращении гироскоп обладает моментом импульса

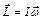. (12.1)

В этом выражении 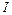– момент инерции гироскопа относительно оси симметрии AA', 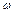– угловая скорость его вращения относительно той же оси. Отметим, что векторы 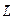и 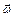расположены вдоль оси вращения. Их направление определяется правилом буравчика. Движение гироскопа с неподвижным центром масс описывается уравнением моментов или основным уравнением динамики вращательного движения:

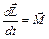. (12.2)

В котором 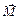– равнодействующая моментов внешних сил, приложенных к телу. Момент силы равен векторному произведению радиуса вектора точки, к которой приложена сила, на эту силу:

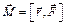. (12.3)

При 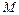= 0 момент импульса сохраняется по величине и направлению. Если к оси гироскопа на некотором расстоянии от его центра масс под углом к этой оси приложить внешнюю силу 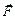, то возникнет момент внешних сил 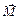(рис.12.2), направленный перпендикулярно вектору 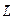. Из уравнения (12.2) следует, что векторы 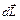и 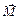параллельны друг другу, поэтому 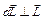. Из сказанного следует, что внешняя сила изменяет только направление момента импульса, не меняя его величины, т. е. заставляет его вращаться вокруг своего направления. Таким образом, момент импульса, а с ним и ось AA' гироскопа, описывает в пространстве коническую поверхность (рис.12.2, а).

За время 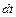проекция момента импульса на горизонтальную плоскость повернется на угол :

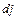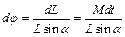, (12.4)

где 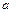– угол между направлениями момента импульса и оси вращения.

Угловая скорость 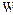вращения вектора 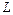вокруг направления внешней силы

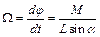. (12.5)

Выразим значение момента силы 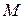из написанной выше формулы:

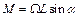. (12.6)

Учтем, что величины 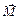, 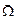и 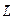являются векторами, их направления показаны на рис.2, и перепишем формулу (6) в векторной форме:

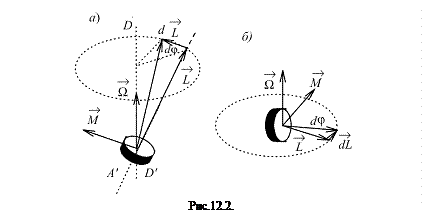
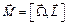. (12.7)

В дальнейшем внешней силой, приложенной к гироскопу, будет сила тяжести дополнительного груза, направленная вертикально вниз. Под действием момента этой силы ось гироскопа будет вращаться вокруг вертикальной оси DD' с угловой скоростью 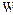(см. рис.12.2). Поскольку при этом вращении взаимная ориентация векторов 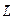и не изменяется, вращение гироскопа вокруг вертикальной оси DD' будет равномерным. Такое вращение называется регулярной прецессией, а величина – угловой скоростью прецессии.

Если ось гироскопа AA' направлена горизонтально (рис.12.2, б), т. е. 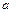= 90° и коническая поверхность становится плоской, то из уравнения (12.6) следует, что

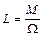. (12.8)

Отметим, что все приведенные выше рассуждения относятся к быстро вращающемуся гироскопу, когда 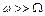. В настоящей работе это условие выполняется.