Статистический смысл энтропии

Из уравнения Гиббса – Гельмгольца:

.

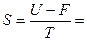
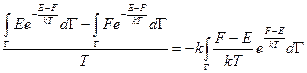Обозначим 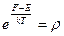; 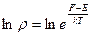, и, т. к. функция распределения 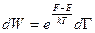, используем выражение для среднего:

.

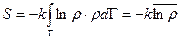Записанное выражение отражает статистический смысл энтропии. Энтропия прямо пропорциональна среднему значению логарифма функции распределения.

Анализируя статистический смысл энтропии, рассмотрим следующий пример.

Допустим, есть два объема: 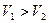, причем в объемах содержится одинаковое количество молекул .

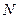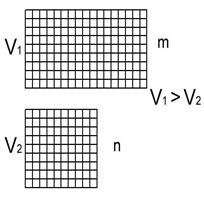
Введем достаточно маленький объемчик 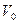и разобьем 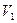и 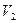на такие элементарные объемы.

В первом случае получим 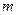-ячеек, во втором 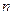-ячеек. Одну молекулу можно распределить 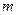-способами в 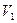и 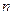-способами в .

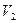Тогда в первом случае: 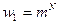, во втором: .

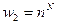Найдем отношение .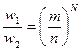

,

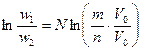(2) .

.

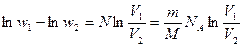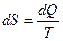Рассмотрим переход газа при изотермическом процессе от 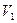до :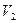

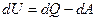(первый закон термодинамики).

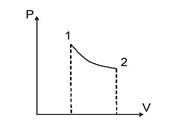
В изотермическом процессе ,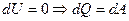

,

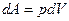Из уравнения Менделеева: ,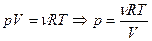

,

,

.

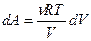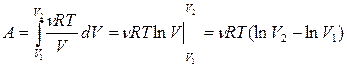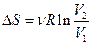Чтобы было соответствие с рисунком, переобозначим точки:

(3) .

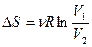Сравним (2) и (3).

Домножим обе части (2) на :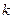

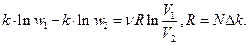
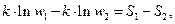
Энтропия пропорциональна числу возможных способов размещения в объеме.

Число возможных различных состояний 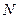будем называть термодинамической вероятностью.