по дисциплине «Математика 2»
модулей «Высшая математика», «Высшая математика и физика»
для студентов 1 курса политехнического и машиностроительного факультетов
специальностей 5В073000 – «Производство строительных материалов, изделий и конструкций», 5В072900 – «Строительство», 5В072400 – «Технологические машины и оборудования», 5В071600 – «Приборостроение», 5В073100 – «Безопасность жизнедеятельности и охрана окружающей среды»
форма обучения очная
на 2 семестр 2014-2015 учебного года
- Перечень вопросов и заданий итогового контроля
| № | Уровень сложности | Вопросы | Тема | A | B | C | D | E | F | G | H |
| 1. | Найти частные производные функции 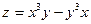 . .
| 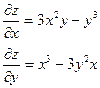
| 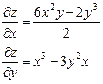
| 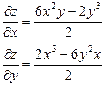
| 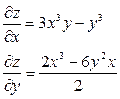
| 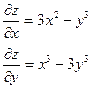
| 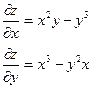
| 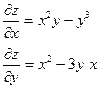
| 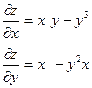
| ||
| 2. | Частная производная первого порядка по переменной х (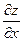 ) функции ) функции 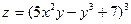
| 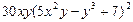
| 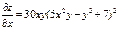
| 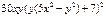
| 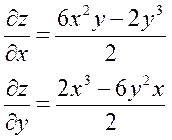
| 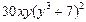
| 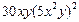
| 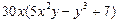
| 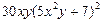
| ||
| 3. | Частная производная первого порядка по переменной у (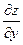 ) функции ) функции 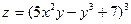
| 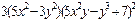
| 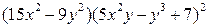
| 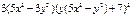
| 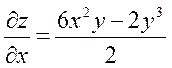
| 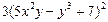
| 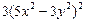
| 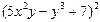
| 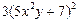
| ||
| 4. | Частная производная первого порядка по переменной х (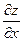 ) функции z= ) функции z= 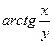 . .
| 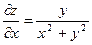
| 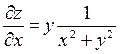
| 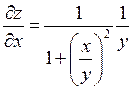
| 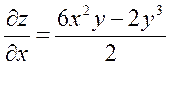
| 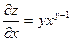
| 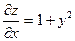
| 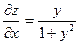
| 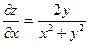
| ||
| 5. | Частная производная первого порядка по переменной у (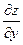 ) функции z= ) функции z= 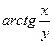 . .
| 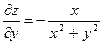
| 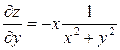
| 
| 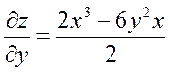
| 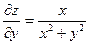
| 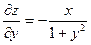
| 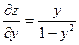
| 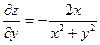
| ||
| 6. | Найти частные производные функции 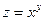 . .
| 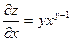 ; ; 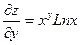
| 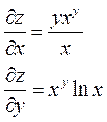
| 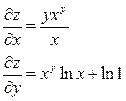
| 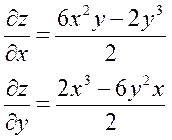
| 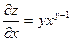 ; ; 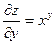
| 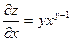 ; ; 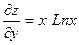
| 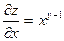 ; ; 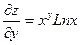
| 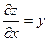
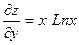
| ||
| 7. | Частная производная первого порядка по переменной 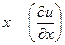 функции функции 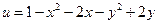 равна: равна:
| 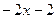
| 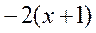
| 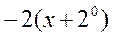
| 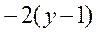
| 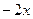
| 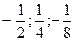
| 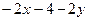
| |||
| 8. | Частная производная первого порядка по переменной у (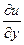 ) функции ) функции 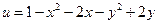
| -2у+2 | 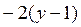
| 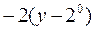
| 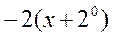
| 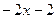
| 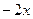
| 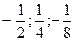
| 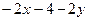
| ||
| 9. | Частная производная первого порядка по переменной 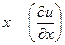 функции функции 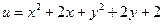 равна: равна:
| 2х+2 | 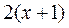
| 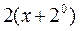
| 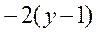
| 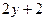
| 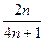
| 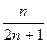
| |||
| 10. | Частная производная первого порядка по переменной
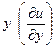 функции функции 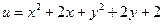 равна: равна:
| 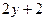
| 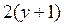
|
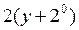
| 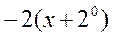
| 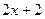
| 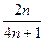
| 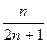
| |||
| 11. | Частная производная первого порядка по переменной 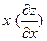 функции функции 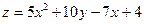 равна: равна:
| 10х-7 | 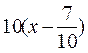
| 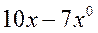
| 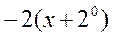
| 24х+24-7 | 24х | 24y | |||
| 12. | Частная производная первого порядка по переменной 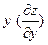 функции
функции 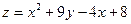 равна: равна:
| 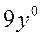
| 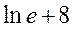
| 2x | 2x+y | 2y | X2+9 | ||||
| 13. | Найти частные производные функции 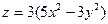
| 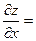 30х, 30х, 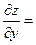 -18у -18у
| 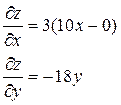
| 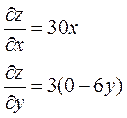
| 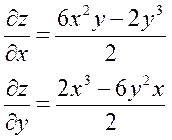
| 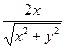
| 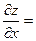 30x 30x
| 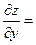 18у 18у
| 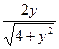
| ||
| 14. | Частная производная первого порядка по переменной 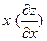 функции функции 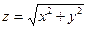 равна: равна:
| 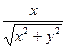
| 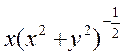
| 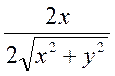
| 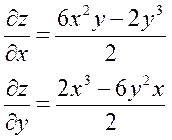
| 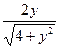
| 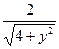
| 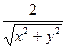
| 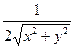
| ||
| 15. | Частная производная первого порядка по переменной 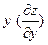 функции
функции 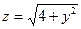 равна: равна:
| 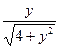
| 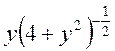
| 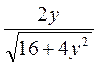
| 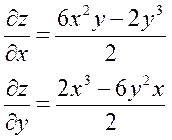
| 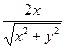
| 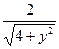
| 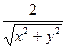
| 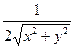
| ||
| 16. | Найти частные производные функции 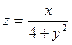
| 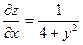 , , 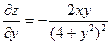
| 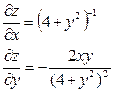
| 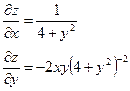
| 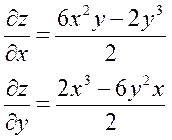
| 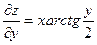
| 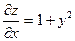
| 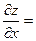 30x 30x
| 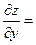 18у 18у
| ||
| 17. | Найти частные производные функции 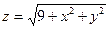
| 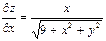 , , 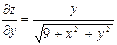
| 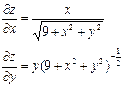
| 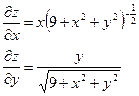
| 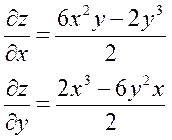
| 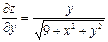 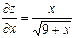
| 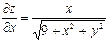 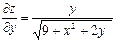
| 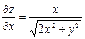 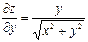
| 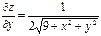 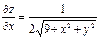
| ||
| 18. | Найти проекции градиента 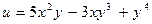 в произвольной точке. в произвольной точке.
| 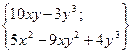
| 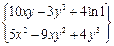
| 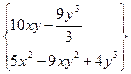
| 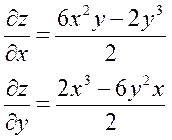
| 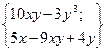
| 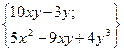
| 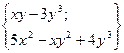
| 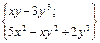
| ||
| 19. | Найти проекции градиента  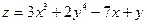 в произвольной точке в произвольной точке
| {9x2-7; 8y3+1} | 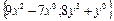
| 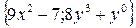
| 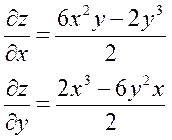
| 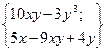
| {9x2;8y3+1} | {9x2 ; 8y3} | {9x2-7; 8y3} | ||
| 20. | Найти проекции градиента  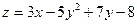 в произвольной точке в произвольной точке
| {3; -10y+7} | 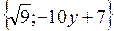
| 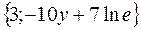
| 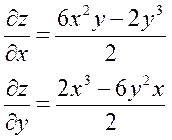
| {3; -24} | {3х; -24y+7} | {3х; -24y} | {3; -24y-7} | ||
| 21. | 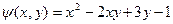 . Найти проекции градиента в точке (1;2). . Найти проекции градиента в точке (1;2).
| {-2;1} | 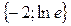
| 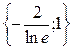
| 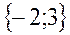
| {-4;5} | {-3;-4} | {-1;4} | {-2;4} | ||
| 22. | 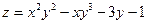 . Найти проекции градиента в точке (2,1) . Найти проекции градиента в точке (2,1)
| {3,-1} | 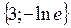
| 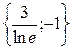
| 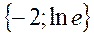
| {-4;5} | {-2;1} | {-3;-4} | {-2;4} | ||
| 23. | 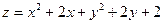 . Найти проекции градиента в точке (1,1) . Найти проекции градиента в точке (1,1)
| {4,4} | 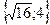
|
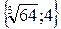
| 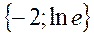
| {-2;1} | {-3;-4} | {-4;5} | {-2;4} | ||
| 24. | 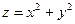 . Найти . Найти 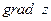 в точке (3;2). в точке (3;2).
| 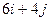
| 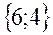
| 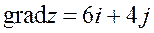
| 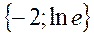
| 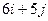
| 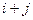
| 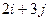
| 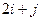
| ||
| 25. | 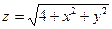 . Найти . Найти 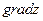 в точке (2;1). в точке (2;1).
| 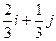
| 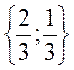
| 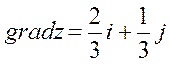
| 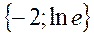
| 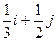
| 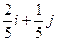

| 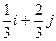
| 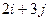
| ||
| 26. | Найти производную функции 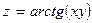 в точке (1;1) в направлении биссектрисы первого координатного угла. в точке (1;1) в направлении биссектрисы первого координатного угла.
| 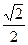
| 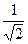
| 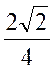
| 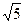
| 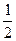
| 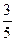
| 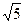 +2 +2
| |||
| 27. | Найти производную функции 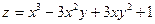 в точке М(3;1) в направлении, идущем от этой точки к точке (6;5). в точке М(3;1) в направлении, идущем от этой точки к точке (6;5).
| 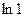
| 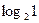
| -1 | -2 | ||||||
| 28. | Найти производную функции 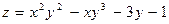 в точке (2;1) в направлении, идущем от этой точки к началу координат. в точке (2;1) в направлении, идущем от этой точки к началу координат.
| - 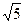
| 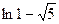
| 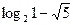
| 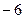
| 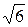
| |||||
| 29. | Какую замену надо использовать для решения однородного дифференциального уравнения первого порядка? | 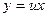
| 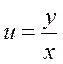
| 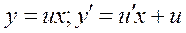
| 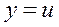
| 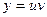
| 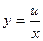
| 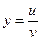
| 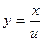
| ||
| 30. | Чтобы понизить порядок дифференциального уравнения 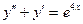
| 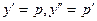
| 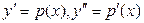
| 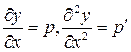
| 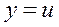
| 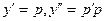
| 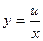
| 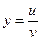
| 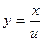
| ||
| 31. | Укажите общее решение однородного линейного уравнения, соответствующего уравнению 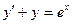
| 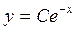
| 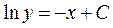
| 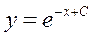
| 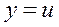
| 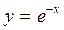
| 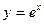
| 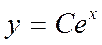
| 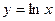
| ||
| 32. | Чтобы понизить порядок дифференциального уравнения 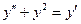 необходимо использовать замену необходимо использовать замену
| 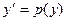
| 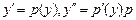
| 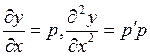
| 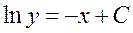
| 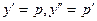
| 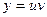
| 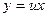
| 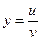
| ||
| 33. | Найдите частное решение дифференциального уравнения 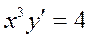 удовлетворяющее начальному условию удовлетворяющее начальному условию 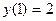
| 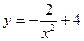
| 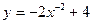
| 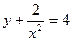
| 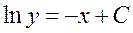
| 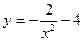
| 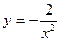
| 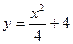
| 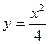
| ||
| 34. | Какие из следующих дифференциальных уравнений первого порядка являются линейными: | 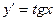
| 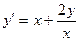
| 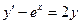
| 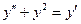
| 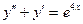
| 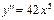
| 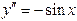
| 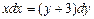
| ||
| 35. | Решить дифференциальное уравнение: 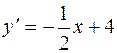
| 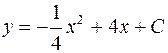
| 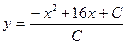
| 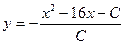
| 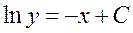
| 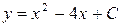
| 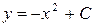
| 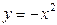
| 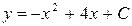
| ||
| 36. | Решить дифференциальное уравнение: 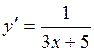
| 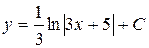
| 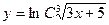
| 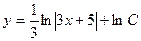
| 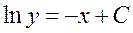
| 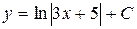
| 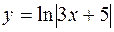
| 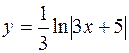
| 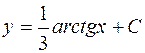
| ||
| 37. | Решить дифференциальное уравнение: 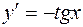
| 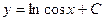
| 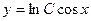
| 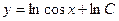
| 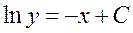
| 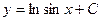
| 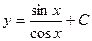
| 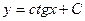
| 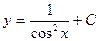
| ||
| 38. | Решить дифференциальное уравнение: 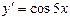
| 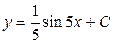
| 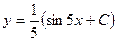
| 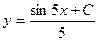
| 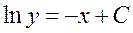
| 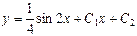
| 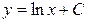
| 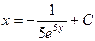
| 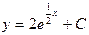
| ||
| 39. | Решить дифференциальное уравнение: 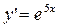
| 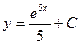
| 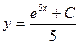
| 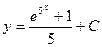
| 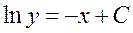
| 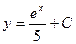
| 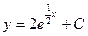
| 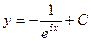
| 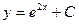
| ||
| 40. | Решить дифференциальное уравнение: 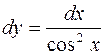
| 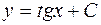
| 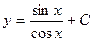
| 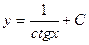
| 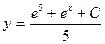
| 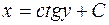
| 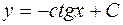
| 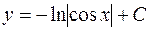
| 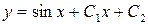
| ||
| 41. | Решить дифференциальное уравнение: 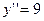
| 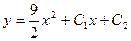
| 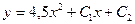
| 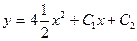
| 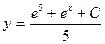
| 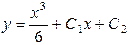
| 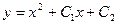
| 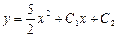
| 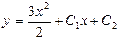
| ||
| 42. | Решить дифференциальное уравнение: 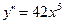
| 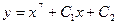
| 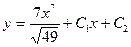
| 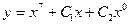
| 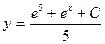
| 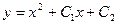
| 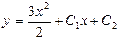
| 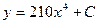
| 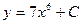
| ||
| 43. | Решить дифференциальное уравнение: 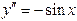
| 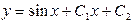
| 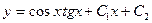
| 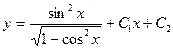
| 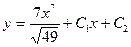
| 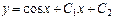
| 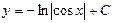
| 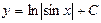
| 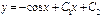
| ||
| 44. | Решить дифференциальное уравнение: 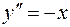
| 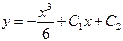
| 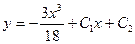
| 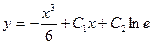
| 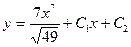
| 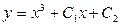
| 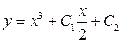
| 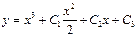
| 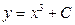
| ||
| 45. | При каком значении к функция 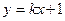 будет решением уравнения будет решением уравнения 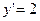
| + 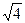
| 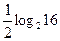
| 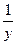
| 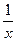
| ||||||
| 46. | При каком значении к функция 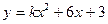 будет решением уравнения будет решением уравнения 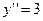
| 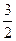
| 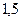
| 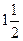
| -3 | 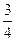
| |||||
| 47. | Решить дифференциальное уравнение: 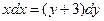
| 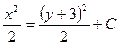
| 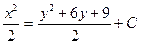
| 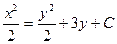
| 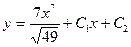
| 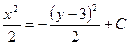
| 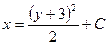
| 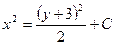
| 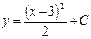
| ||
| 48. | Решить дифференциальное уравнение: 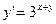
| 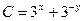
| 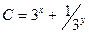
| 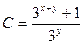
| 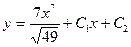
| 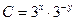
| 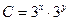
| 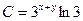
| 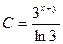
| ||
| 49. | Решить дифференциальное уравнение: 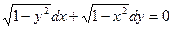
| 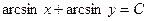
| 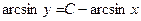
| 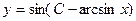
| 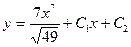
| 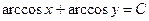
| 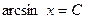
| 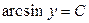
| 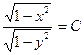
| ||
| 50. | Решить дифференциальное уравнение: 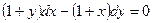
| 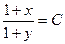
| 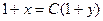
| 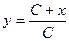
| 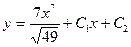
| 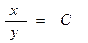
| 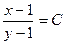
| 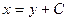
| 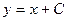
| ||
| 51. | Решить дифференциальное уравнение: 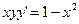
| 
| 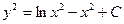
| 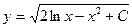
| 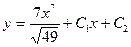
| 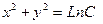
| 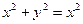
| 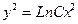
| 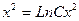
| ||
| 52. | Решить дифференциальное уравнение: 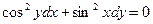
| 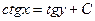
| 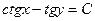
| 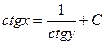
| 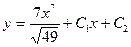
| 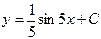
| 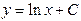
| 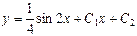
| 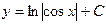
| ||
| 53. | 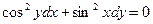 . Какого порядка дифференциальное уравнение? . Какого порядка дифференциальное уравнение?
| 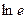
| 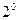
| ||||||||
| 54. | Какие из следующих уравнении являются уравнениями с разделяющимися переменными | 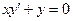
| 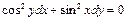
| 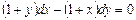
| 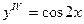
| 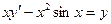
| 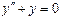
| 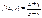
| 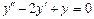
| ||
| 55. | Какие из следующих уравнении являются однородными | 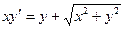
| 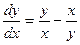
| 
| 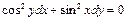
| 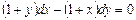
| 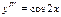
| 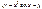
| 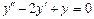
| ||
| 56. | Какие из следующих уравнении являются однородными | 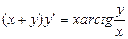
| 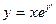
| 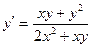
| 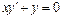
| 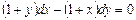
| 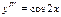
| 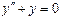
| 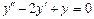
| ||
| 57. | Какие из следующих уравнении являются линейными | 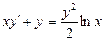
| 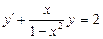
| 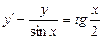
| 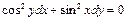
| 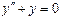
| 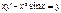
| 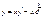
| 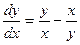
| ||
| 58. | Какие из следующих уравнении являются линейными | 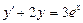
| 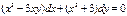
| 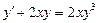
| 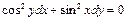
| 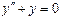
| 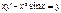
| 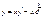
| 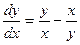
| ||
| 59. | Какие из следующих уравнении являются уравнением Бернулли | 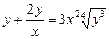
| 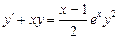
| 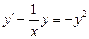
| 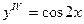
| 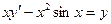
| 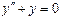
| 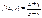
| 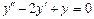
| ||
| 60. | Определить степень однородности функции 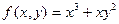
| 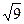
| 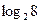
| ||||||||
| 61. | Определить степень однородности функции 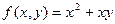
| 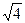
| 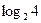
| 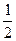
| |||||||
| 62. | Определить степень однородности функции 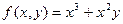
| 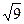
| 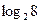
| ||||||||
| 63. | Определить степень однородности функции 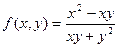
| 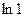
| 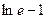
| -1 | |||||||
| 64. | Решить дифференциальное уравнение
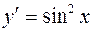
| 
| 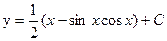
| 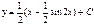
| 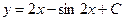
| 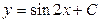
| 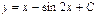
| 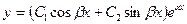
| 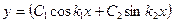
| ||
| 65. | Решить дифференциальное уравнение
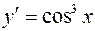
| 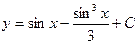
| 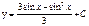
| 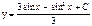
| 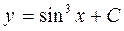
| 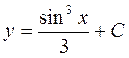
| 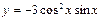
| 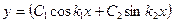
| 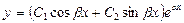
| ||
| 66. | Решить дифференциальное уравнение
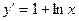
| 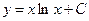
| 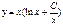
| 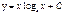
| 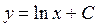
| 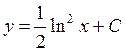
| 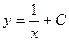
| 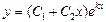
| 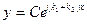
| ||
| 67. | Решить дифференциальное уравнение 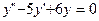
| 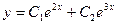
| 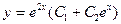
| 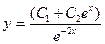
| 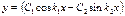
| 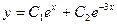
| 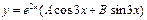
| 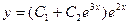
| 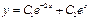
| ||
| 68. | Решить дифференциальное уравнение 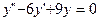
|
 Сейчас читают про:
|
 2015-03-07
2015-03-07 295
295






