Тема 3 Производная
Задачи, приводящие к понятию производной. Производная, ее геометрический, механический и экономический смысл. Уравнение касательной к плоской кривой; Дифференцируемость функции. Связь между дифференцируемостью и непрерывностью функции (необходимый признак дифференцируемости). Основные правила и основные формулы дифференцирования. Производная сложной функции Производные высших порядков. (1, гл. 7, § 7.1 – 7.7, с. 176 – 205); (2, гл. 7).
Необходимо изучить задачи, приводящие к понятию производной: задачи о касательной и задачи о скорости движения (1, с.176, 177), задачи о производительности труда (экономический смысл производной).
После этого нужно усвоить определение производной как предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю. Нужно знать обозначение производной, алгоритм ее вычисления, основываясь на теории пределов.
Студент обязан понимать геометрический и механический смысл производной (1,с.178, 181), уметь решать простейшие задачи по вычислению производной на основе алгоритма ее вычисления; знать и уметь применять основные правила дифференцирования, вычислять производную сложной и обратной функций. При этом нужно знать четко правила вычисления элементарных функций (1,с. 188,193), знать наизусть таблицу производных (1, с.192). Это позволит усвоить дифференцирование сложных функций, обратных функций, неявно заданных функций (1, с.193), находить производные от произведения, суммы, разности, а также вычислять производные высших порядков. Нужно знать использование понятия производной в экономике, понятие эластичности функции, свойства эластичности функции.
Изучая материал этой темы, студенты знакомятся с необходимым условием дифференцируемости функции. Необходимо четко уяснить, что из дифференцируемости функции в некоторой точке следует ее непрерывность в этой точке. Обратная теорема несправедлива, так как существуют непрерывные функции, которые в некоторых точках могут не иметь производной (1, с. 179, 180).
Рекомендуется разобрать задачи с решениями N 7.1–7.8, 7.10, 7.13, 1.15–7.17 и задачи для самостоятельной работы N 7.20–7.29, 7.35, 7 42, 7.43, 7.46–7. 49 по учебнику (1) и аналогичные задачи по практикуму (2).
Для усвоения темы нужно решить задачи контрольной работы, ответить письменно на теоретические вопросы в контрольной работе.
Тема 4 Приложения производной
Правило Лопиталя ('без вывода), Теорема Ролля и Лагранжа (с нестрогими геометрическими доказательствами). Признаки возрастания и убывания функции. Экстремум функции. Необходимые и достаточные признаки экстремума (второй достаточный признак – без доказательства). Исследование функции (область определения, четность и нечетность, интервалы монотонности и точки экстремума, поведение функции при х ®±¥ и в точках разрыва, горизонтальные и вертикальные асимптоты, точки пересечения графика с осями координат) и построние ее графика. Квадратичная функция у = ax2+bx+c и ее график. Дробно-линейная функция у = 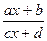 и ее график. (1,гл. 8, § 8.1 – 8.5, 8.7 – 8.9; с. 205–21, 225–236); (2, гл. 8).
и ее график. (1,гл. 8, § 8.1 – 8.5, 8.7 – 8.9; с. 205–21, 225–236); (2, гл. 8).
Нужно уяснить, что правило Лопиталя является эффективным средством вычисления пределов. При этом нужно понимать, что предел отношения двух бесконечно малых или бесконечно больших функций заменяется вычислением отношения их производных. Это правило можно использовать для вычисления целого ряда неопределенностей.
С помощью производных можно эффективно исследовать функции на возрастание и убывание, определять экстремумы функций (1,с.216, 217), наибольшее и наименьшее значение. Для этого необходимо знать теоремы о достаточных условиях возрастания и убывания функции, определения точек минимума и максимума, первое и второе достаточное условие экстремума, определение выпуклости и вогнутости функции (выпуклости вниз). Необходимо знать общую схему исследования функции, кроме п.6,7 (1, с.232).
В учебном пособии приведена схема исследования функции для нахождения характерных точек и особенностей, по которым можно построить ее график (1, с. 232). Выполнение пункта 6' этой схемы, связанного с нахождением интервалов выпуклости функции и точек перегиба, в программу не входит.
Рекомендуется разобрать задачи с решениями е 8.1–8.3, 8.4–8.7; 8.9, 8.11–8.15, 8.17 и задачи для самостоятельной работы N 8.19–8.31, 8.32–8.34, 8 41–8.53 по учебнику (1) и аналогичные задачи по практикуму (2), обратив особое внимание на исследование функций и построение их графиков
Раздел IIИНТЕГРАЛЬНОЕ ИCЧИЛЕНИЕ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
 2015-03-07
2015-03-07 331
331








